Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
[Phương pháp tự luận]
Ta có : y = 6 x 2 - 6 ( m + 1 ) x + 6 m
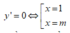
Điều kiện để hàm số có 2 điểm cực trị là m ≠ 1
![]()
Hệ số góc đt AB là k = - ( m - 1 ) 2
Đt AB vuông góc với đường thẳng y = x + 2
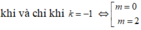

+ Ta có đạo hàm y’ = 6x2- 6( m+ 1) x+ 6m
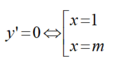
Điều kiện để hàm số có 2 điểm cực trị là : m≠ 1
Tọa độ 2 điểm cực trị là A( 1 ; 3m-1) và B ( m ; -m3+ 3m2)
+ Hệ số góc đường thẳng AB là :k= - ( m-1) 2
+ Đường thẳng AB vuông góc với đường thẳng y= x+ 2 khi và chỉ khi k= -1
Hay – ( m-1) 2= -1( vì 2 đường thẳng vuông góc với nhau thì tích hai hệ số góc bằng -1) 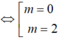
Chọn C.

Chọn D.
![]() TXĐ: D = R.
TXĐ: D = R.
![]()
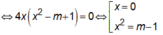
Đồ thị hàm số có 3 điểm cực trị ⇔ y' = 0 có ba nghiệm phân biệt ⇔ m -1 > 0 ⇔ m > 1(*)
3 điểm cực trị của đồ thị hàm số là: A(0;1),
Hàm số đã cho là hàm số chẵn nên đồ thị hàm số nhận Oy làm trục đối xứng
![]()
![]()
![]()
![]()
Ta có
![]()
![]()
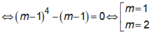
Kết hợp với điều kiện (*) => m = 2
Làm theo bào toán trắc nghiệm như sau:
Hàm số đã cho có 3 điểm cực trị khi ab < 0 ![]()
Chỉ có đáp án D thỏa mãn.

+ Ta có: y’ = 6x2-6( 2m+1) x+ 6m(m+1)
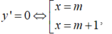
do đó hàm số luôn có cực đại cực tiểu với mọi m.
+ Tọa độ các điểm CĐ, CT của đồ thị là A( m; 2m3+3m2+1 ) và B( m+1; 2m3+3m2)
Suy ra AB = √2 và phương trình đường thẳng AB: x+ y-2m3-3m2-m-1=0.
+ Do đó, tam giác MAB có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ M tới AB nhỏ nhất.
d ( M , A B ) = 3 m 2 + 1 2 ⇒ d ( M , A B ) ≥ 1 2 ⇒ m i n d ( M , A B ) = 1 2
đạt được khi m=0
Chọn B

Chọn B
Ta có:
![]()
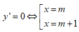
⇒ ∀ m ∈ ℝ , hàm số luôn có CĐ, CT
Tọa độ các điểm CĐ, CT của đồ thị là
![]()
Suy ra A B = 2
và phương trình đường thẳng x + y - 2 m 3 - 3 m 2 - m - 1 = 0
Do đó, tam giác MAB có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ M tới AB nhỏ nhất.
Ta có:
![]()
![]()
⇒ đạt được khi m = 0
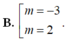
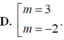
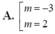

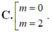
Chọn A