Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Th1 : P = 2 => P + 10 = 12 chia hết cho 2 => P là hợp số < Loại >
Th2 : P > 2 => P sẽ có dạng là : 3k ; 3k +1 ; 3k + 2 ( k thuộc N*)
+, Với P = 3k => P = 3 ( P là SNT ) => P + 10 = 13 ; P + 14 = 17 , là SNT < TM >
+ Với P = 3k + 1 => P + 14 = 3k + 1 + 14 = 3k + 15 = 3(k+5) chia hết cho 3 => là hợp số < Loại >
+ Với P = 3k +2 => P + 10 = 3k + 2 + 10 = 3k + 12 = 3(k+4) chia hết cho 3 => là hợp số < Loại >
Vậy P = 3
b, Tương tự

a) Với p=2 => p+10=12 không là số nguyên tố (loại)
Với p=3 => p+10=13 và p+14=17 là các số nguyên tố (thỏa mãn)
p là số nguyên tố lớn hơn hoặc bằng 3
=> p có dạng 3k+1 ; 3k+2 ( k thuộc N*)
Với p=3k+1 => p+14=3k+15 chia hết cho 3 (loại)
Với p=3k+2 => p+10=3k+12 chia hết cho 3 (loại)
Vậy p=3.
a) Nếu p =2 thì p+10= 12; p+14= 16 ( loại)
Vì p là số nguyên tố nên p có dạng 3k; 3k+1; 3k+2
Nếu p =3k thì p = 3 ( vì p là số nguyên tố) khi đó: p+10 = 13; p+14=17
Nếu p=3k+2 thì p+10= 3k+2+10= 3k+12= 3( k+4) ( vì 3 chia hết cho 3 nên 3(k+4) chia hết cho 3=> p+10 là hợp số trái với đề bài)
Nếu p= 3k+1 thì = 3k+1+14= 3k+15= 3(k+5) (vì...................................................................................................................)
Vậy.......
Chỗ vì thì bn vì như dòng trên nha, còn phần b làm tương tự

1. Vì p là số nguyên tố và p + 10 và p + 14 còng là số nguyên tố nên p > 2 .Mặt khỏc p có thể rơi vào một trong 3 khả năng hoặc p = 3k , p = 3k + 1, p = 3k – 1
- Với p = 3k + 1 thì
p + 14 = 3k + 15 = 3(k + 5 ) ⋮ 3
- Với p = 3k – 1 thì
p + 10 = 3k + 9 = 3 (k + 3) ⋮ 3
Vậy p = 3k . Do p là nguyên tố nên p = 3
2. Xét các trường hợp sau.
- Với p = 5 thì
p + 2 = 7
p + 6 = 11
p + 8 = 13
p + 12 = 17
p + 14 = 19
- Với p > 5 thì p = 5k +1, p = 5k + 2, p = 5k + 3, p = 5k +4
+ Nếu p= 5k +1 thì p + 14 = 5k + 15 ⋮ 5
+ Nếu p = 5k + 2 thì p + 8 = 5k + 10 ⋮ 5
+ Nếu p = 5k + 3 thì p + 12 = 5k + 15 ⋮ 5
+ Nếu p = 5k +4 thì p + 6 = 5k + 10 ⋮ 5
Suy ra nguyên tố cần Tìm là p = 5.

xét p = 2 =>p+10 là hợp số =>ko tm
xét p = 3=>p+10=13,p+14=17 tm
xét p>3 => p=3k+1,p=3k+2
- nếu p = 3k+1 thì p+14 = 3k+15 chia hết cho 3 mà 3k+1>3=>p=3k+1 ko tm
- nếu p=3k+2 thì p+10 = 3k+12 chia hết cho 3 mà 3k+2>3=>p=3k+2 ko tm
a) P+10 và P+14
+ Nếu P=2=> P+10=12; P+14=16(loại)
- Nếu P=3=> P+10=13; P+14=17(tm)
Nếu P>3=> P có dạng 3k;3k+1;3k+2
+Với P=3k mà P>3=> k>1=> P là hợp số ( loại)
+Với P=3k+1=> P+14=3k+1+14=3k+15 chia hết cho 3( loại)
+Với P=3k+2=> P+10=3k+2+10=3k+12 chia hết cho 3( loại)
Vậy với P=3 thì P+10 và P+14 là số nguyên tố.
Các phần còn lại bn làm tương tự
Thấy đúng thì tk nha, thanks nhìu ^_^

Câu b:

Đến đoạn này cũng xét như câu a
Câu c:
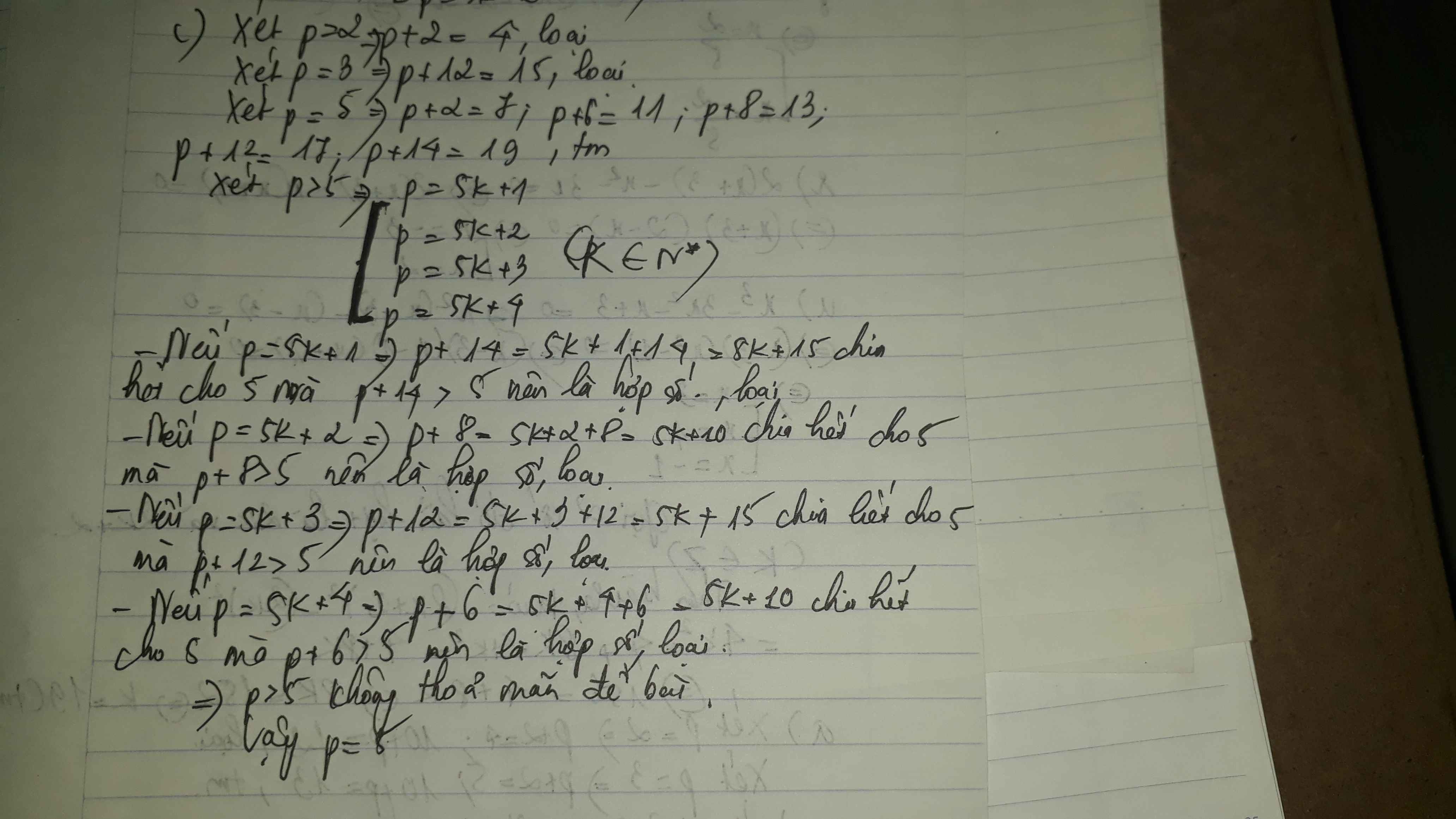


a) do p là số nguyên tố => p lớn hơn hoặc bằng 2
xét p = 2 => p + 2 = 4 (ko là số nguyên tố) ; p+10 = 12 (ko là số nguyên tố)
xét p = 3 => p + 2 = 5 (là số nguyên tố) ; p + 10 = 13 (là số nguyên tố)
=> p = 3 thỏa mãn đề bài
còn lại tương tự nhé!!
t i c k nhé!! 45436457457568658797690807805688568568567467476856845765
b) => p = 3 thỏa mãn đề bài
c) ; d) bn vẫn cứ xét bắt đầu từ 2 rồi lên là sẽ tìm ra!!
654745768765876968987070789078976958567845745745745