1, \(\dfrac{x-1}{2009}+\dfrac{x-2}{2008}=\dfrac{x-3}{2007}+\dfrac{x-4}{2006}\)

\(\Leftrightarrow\left(\dfrac{x-1}{2009}-1\right)+\left(\dfrac{x-2}{2008}-1\right)=\left(\dfrac{x-3}{2007}-1\right)+\left(\dfrac{x-4}{2006}-1\right)\) ( Trừ mỗi vế cho 2 ta được phương trình như này nhé ! )

\(\Leftrightarrow\dfrac{x-2010}{2009}+\dfrac{x-2010}{2008}=\dfrac{x-2010}{2007}+\dfrac{x-2010}{2006}\)

\(\Leftrightarrow\dfrac{x-2010}{2009}+\dfrac{x-2010}{2008}-\dfrac{x-2010}{2007}-\dfrac{x-2010}{2006}=0\)

\(\Leftrightarrow\left(x-2010\right)\left(\dfrac{1}{2009}+\dfrac{1}{2008}-\dfrac{1}{2007}-\dfrac{1}{2006}\right)=0\)

Do \(\dfrac{1}{2009}+\dfrac{1}{2008}-\dfrac{1}{2007}-\dfrac{1}{2006}\ne0\) nên \(x-2010=0\Leftrightarrow x=2010\)

2, \(\dfrac{59-x}{41}+\dfrac{57-x}{43}+\dfrac{55-x}{45}+\dfrac{53-x}{47}+\dfrac{51-x}{49}=-5\)

​\(\left(\dfrac{59-x}{41}+1\right)+\left(\dfrac{57-x}{43}+1\right)+\left(\dfrac{55-x}{45}+1\right)+\left(\dfrac{53-x}{47}+1\right)+\left(\dfrac{51-x}{49}+1\right)=0\)

đề sai rồi. ko có y mà lại tìm y ở đâu ra thế

(x+2)+(4x+4)+(7x+6)+...+(25x+18)+(28x+20)=1560

(x+4x+7x+...+25x+28x)+(2+4+6+..+18+20)=1560

145x+110=1560

145x=1450

x=10

vậy........

Bài 1 :

Gọi \(A=5+5^2+5^3+...+5^{98}+5^{99}\\ 5A=5^2+5^3+5^4+...+5^{99}+5^{100}\\ 5A-A=\left(5^2+5^3+5^4+...+5^{99}+5^{100}\right)-\left(5+5^2+5^3+...+5^{98}+5^{99}\right)\\ 4A=5^{100}-5\\ A=\dfrac{5^{100}-5}{4}\)

Bài 2:

\(\left(12x-4\right)\cdot8^{2022}=4\cdot8^{2023}\\ 12x-4=4\cdot8^{2023}:8^{2022}\\ 12x-4=4\cdot8\\ 12x-4=32\\ 12x=36\\ x=3\)

Bài 2: 

Ta có: (x-3)(x+4)>0

=>x>3 hoặc x<-4

Bài 3:

a: \(5S=5-5^2+...+5^{99}-5^{100}\)

\(\Leftrightarrow6S=1-5^{100}\)

hay \(S=\dfrac{1-5^{100}}{6}\)

Lời giải:
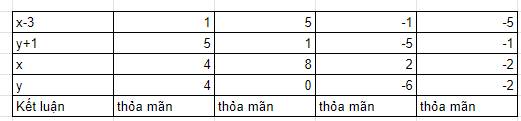
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:

b.

$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$

$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$

$=2+24+(1+5)(5^2+5^4+...+5^{98}$

$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$

$\Rightarrow A$ chia $6$ dư $2$.

1.3.5.7........99 = \(\frac{\left(1.3.5.7......99\right)\left(2.4.6......100\right)}{2.4.6......100}\)= \(\frac{1.2.3......99.100}{2^{50}\left(1.2.3.....50\right)}=\frac{51.52.53.......100}{2.2.2......2}=\frac{51}{2}.\frac{52}{2}....\frac{100}{2}\)(ĐPCM)

                                      50 số 2

ko hiểu

  A= 1 + 5 + 5² + 5 ³ + ... + 5⁸⁰⁰ 

5A=       5 + 5²  + 5³ + .... +5 ⁸⁰⁰ + 5⁸⁰¹  

5A - A = 5⁸⁰¹  - 1 

4a = 5⁸⁰¹ - 1 

    5⁸⁰¹ - 1 +1 = 5ⁿ

⇒  5⁸⁰¹ = 5ⁿ ⇒ n = 801