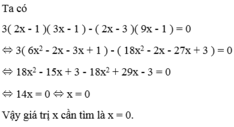
\(a,\left(x-3\right)\left(x^2+3x+9\right)+x\left(x+2\right)\left(2-x\right)=0\\ \Rightarrow\left(x^3-27\right)+x\left(4-x^2\right)=0\\ \Rightarrow x^3-27+4x-x^3=0\\ \Rightarrow4x-27=0\\ \Rightarrow4x=27\\ \Rightarrow x=\dfrac{27}{4}\)

\(b,\left(x+1\right)^3-\left(x-1\right)^3-6\left(x-1\right)^2=-10\\ \Rightarrow\left(x^3+3x^2+3x+1\right)-\left(x^3-3x^2+3x-1\right)-6\left(x^2-2x+1\right)=-10\\ \Rightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+12x-6+10=0\)

\(\Rightarrow12x+6=0\\ \Rightarrow12x=-6\\ \Rightarrow x=-\dfrac{1}{2}\)

\(x^2-3x+2.\left(x-3\right)=0\)

\(x.\left(x-3\right)+2.\left(x-3\right)=0\)

\(\left(x-3\right).\left(x+2\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x=3\\x=-2\end{cases}}\)

\(x.\left(x-3\right)-3x+9=0\)

\(x.\left(x-3\right)-3.\left(x-3\right)=0\)

\(\left(x-3\right)^2=0=>x=3\)

a,\(x^2-3x+2\left(x-3\right)=0.\)

\(\Leftrightarrow x^2-3x+2x-6=0\)

\(\Leftrightarrow x^2+x-6=0\)

\(\Leftrightarrow\left(x^2-2x\right)+\left(3x-6\right)=0\)

\(\Leftrightarrow x\left(x-2\right)+3\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x+3\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x+3=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=2\\x=-3\end{cases}}\)

\(\left(x-1\right)^3-\left(x+3\right)\left(x^2-3x+9\right)+3\left(x-2\right)\left(x+2\right)=0\)

\(\Leftrightarrow x^3-3x^2+3x-1-x^3-27+3x^2-12=0\)

\(\Leftrightarrow3x=40\)

hay \(x=\dfrac{40}{3}\)

a) Tìm được x = -4.        

b) Tìm được x = 3.

c) Tìm được x = ±1.

\(\left(2x-1\right)^2-\left(x+3\right)^2=0\)

\(\Leftrightarrow\left(2x-1-x-3\right)\left(2x-1+x+3\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left(3x+2\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-4=0\\3x+2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=4\\x=-\frac{2}{3}\end{cases}}}\)

\(x^3+27+\left(x+3\right)\left(x-9\right)=0\)

\(\Leftrightarrow\left(x+3\right)\left(x^2-3x+9\right)+\left(x+3\right)\left(x-9\right)=0\)

\(\Leftrightarrow\left(x+3\right)\left(x^2-3x+9+x-9\right)=0\)

\(\Leftrightarrow\left(x+3\right)\left(x^2-2x\right)=0\)

\(\Leftrightarrow x\left(x+3\right)\left(x-2\right)=0\)

\(\Leftrightarrow\hept{\begin{cases}x=0\\x+3=0\\x-2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\x=-3\\x=2\end{cases}}}\)

a) Ta có: \(\left(x-2\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+6\left(x+1\right)^2=15\)

\(\Leftrightarrow x^3-6x^2+12x-8-x^3+27+6\left(x^2+2x+1\right)=15\)

\(\Leftrightarrow-6x^2+12x+19+6x^2+12x+6=15\)

\(\Leftrightarrow24x+25=15\)

\(\Leftrightarrow24x=-10\)

hay \(x=-\dfrac{5}{12}\)

b) Ta có: \(2x^3-50x=0\)

\(\Leftrightarrow2x\left(x-5\right)\left(x+5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)

c) Ta có: \(5x^2-4\left(x^2-2x+1\right)-5=0\)

\(\Leftrightarrow5x^2-4x^2+8x-4-5=0\)

\(\Leftrightarrow x^2+8x-9=0\)

\(\Leftrightarrow\left(x+9\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-9\\x=1\end{matrix}\right.\)

d) Ta có: \(x^3-x=0\)

\(\Leftrightarrow x\left(x-1\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)

e) Ta có: \(27x^3-27x^2+9x-1=1\)

\(\Leftrightarrow\left(3x\right)^3-3\cdot\left(3x\right)^2\cdot1+3\cdot3x\cdot1^2-1^3=1\)

\(\Leftrightarrow\left(3x-1\right)^3=1\)

\(\Leftrightarrow3x-1=1\)

\(\Leftrightarrow3x=2\)

hay \(x=\dfrac{2}{3}\)

Một. Khai triển vế trái của phương trình:
(x-3)(x+3) = x(x+3) - 3(x+3) = x^2 + 3x - 3x - 9 = x^2 - 9

Khai triển vế phải của phương trình:
(x-5)^2 = (x-5)(x-5) = x(x-5) - 5(x-5) = x^2 - 5x - 5x + 25 = x^2 - 10x + 25

Đặt hai cạnh bằng nhau:
x^2 - 9 = x^2 - 10x + 25

Trừ x^2 từ cả hai phía:
-9 = -10x + 25

Trừ 25 từ cả hai vế:
-34 = -10 lần

Chia cả hai vế cho -10:
x = 3,4

b. Khai triển vế trái của phương trình:
(2x+1)^2 - 4x(x-1) = (2x+1)(2x+1) - 4x^2 + 4x = 4x^2 + 2x + 2x + 1 - 4x^2 + 4x = 8x + 1

Đặt vế trái bằng 17:
8x + 1 = 17

Trừ 1 cho cả hai vế:
8x = 16

Chia cả hai vế cho 8:
x = 2

c. Khai triển vế trái của phương trình:
(3x-2)(3x+2) - 9(x-1)x = (9x^2 - 4) - 9x^2 + 9x - 9x = -4 + 9x

Đặt vế trái bằng 0:
-4 + 9x = 0

Thêm 4 vào cả hai bên:
9x = 4

Chia cả hai vế cho 9:
x = 4/9

d. Khai triển vế trái của phương trình:
(3-x)^3 - (x+3)^3 = (27 - 9x + x^2) - (x^3 + 9x^2 + 27) = 27 - 9x + x^2 - x^3 - 9x^2 - 27 = -x^3 - 8x^2 - 9x

Đặt vế trái bằng 36x^2 - 54x:
-x^3 - 8x^2 - 9x = 36x^2 - 54x

Cộng x^3 + 8x^2 + 9x vào cả hai vế:
0 = 37x^2 - 63x

Chia cả hai vế cho x:
0 = 37x - 63

Thêm 63 vào cả hai bên:
63 = 37 lần

Chia cả hai vế cho 37:
x = 63/37

a, 5x . (x - 3) + x - 3 = 0

<=> 5x . (x - 3) + (x - 3) = 0

<=> (x - 3)(5x + 1) = 0

<=> x - 3 = 0 hoặc 5x + 1 = 0

<=> x = 3               5x = -1

<=> x = 3                x = -1/5

Vậy...

b,   (x + 2)² + (x - 3)² - 2(x - 1)(x + 1) = 9

<=> x² + 4x + 4 + x² - 6x + 9 - 2(x² - 1²) = 9

<=> 2x² - 2x + 13 - 2x² + 2 = 9

<=> -2x + 15 = 9

<=> -2x = -6

<=> x = 3

\(a)\)\(x^3-x^2-x+1=0\)

\(\Leftrightarrow\)\(x^2\left(x-1\right)-\left(x-1\right)=0\)

\(\Leftrightarrow\)\(\left(x-1\right)\left(x^2-1\right)=0\)

\(\Leftrightarrow\)\(\left(x-1\right)\left(x-1\right)\left(x+1\right)=0\)

\(\Leftrightarrow\)\(\left(x-1\right)^2\left(x+1\right)=0\)

\(\Leftrightarrow\)\(\orbr{\begin{cases}\left(x-1\right)^2=0\\x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=-1\end{cases}}}\)

Vậy \(x=1\) hoặc \(x=-1\)

Chúc bạn học tốt ~ 

a) x³-x²-x+1 = 0 \(\Leftrightarrow x^2\left(x-1\right)-\left(x-1\right)=0\)

\(\Leftrightarrow\left(x^2-1\right)\left(x-1\right)=0\)\(\Leftrightarrow x^2-1=0\)hoặc x-1=0 

\(\Leftrightarrow x=1\)

a) 3x^3-12x=0

3x(x^2-4)=0

3x(x-2)(x+2)=0

suy ra 3x=0       suy ra x=0

           x-2=0               x=2

           x+2=0              x= -2

b) (x-3)^2-(x-3)(3-x)^2=0

(x-3)^2-(x-3)(x-3)^2=0

(x-3)^2(1-x+3)=0

(x-3)^2(4-x)=0

suy ra x-3=0  suy ra x=3

          4-x=0             x=4

a) và b) đã nhé bạn