Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt 3759=a; 5741=b
Theo đề, ta có: \(E=4\dfrac{7}{b}\cdot\dfrac{1}{a}-\dfrac{4}{a}\cdot\left(1+\dfrac{2}{b}\right)+\dfrac{1}{a}+\dfrac{1}{ab}\)
\(=\dfrac{4b+7}{b}\cdot\dfrac{1}{a}-\dfrac{4}{a}\cdot\dfrac{b+2}{b}+\dfrac{b+1}{ab}\)
\(=\dfrac{4b+7-4b-8+b+1}{ab}=\dfrac{b}{ab}=\dfrac{1}{a}=\dfrac{1}{3759}\)

bài 1: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{x}{x+2}-\dfrac{x}{x-2}\)
\(=\dfrac{x\left(x-2\right)-x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2-2x-x^2-2x}{\left(x-2\right)\left(x+2\right)}=-\dfrac{4x}{x^2-4}\)
Bài 2:
1: \(x^2y^2-8-1\)
\(=x^2y^2-9\)
\(=\left(xy-3\right)\left(xy+3\right)\)
2: \(x^3y-2x^2y+xy-xy^3\)
\(=xy\cdot x^2-xy\cdot2x+xy\cdot1-xy\cdot y^2\)
\(=xy\left(x^2-2x+1-y^2\right)\)
\(=xy\left[\left(x-1\right)^2-y^2\right]\)
\(=xy\left(x-1-y\right)\left(x-1+y\right)\)
3: \(x^3-2x^2y+xy^2\)
\(=x\cdot x^2-x\cdot2xy+x\cdot y^2\)
\(=x\left(x^2-2xy+y^2\right)=x\left(x-y\right)^2\)
4: \(x^2+2x-y^2+1\)
\(=\left(x^2+2x+1\right)-y^2\)
\(=\left(x+1\right)^2-y^2\)
\(=\left(x+1+y\right)\left(x+1-y\right)\)
5: \(x^2+2x-4y^2+1\)
\(=\left(x^2+2x+1\right)-4y^2\)
\(=\left(x+1\right)^2-4y^2\)
\(=\left(x+1-2y\right)\left(x+1+2y\right)\)
6: \(x^2-6x-y^2+9\)
\(=\left(x^2-6x+9\right)-y^2\)
\(=\left(x-3\right)^2-y^2=\left(x-3-y\right)\left(x-3+y\right)\)

B1: a)\(xy\left(3x-2y\right)-2xy^2=3x^2y-2y^2x-2xy^2=3x^2y-4xy^2\)
b) \(\left(x^2+4x+4\right):\left(x+2\right)=\left(x+2\right)^2:\left(x+2\right)=\left(x+2\right)\)
\(\dfrac{2\left(x-1\right)}{x^2}.\dfrac{x}{\left(x-1\right)}=\dfrac{2\left(x-1\right)x}{x^2\left(x-1\right)}=\dfrac{2}{x}\)
B2:
a)\(2x^2-4x+2=2\left(x^2-2x+1\right)=2\left(x-1\right)^2\)
b)\(x^2-y^2+3x-3y=\left(x-y\right)\left(x+y\right)+3\left(x-y\right)=\left(x-y\right)\left(x+y+3\right)\)
Mấy bài này là mấy bài rất rất rất cơ bản, học sinh TB cũng phải tự làm được, mấy bài kiểu này đừng nên đăng lên hỏi nha:vv

a, \(\dfrac{x^2}{4}-xy+y^2=\left(\dfrac{x}{2}\right)^2-xy+y^2=\left(\dfrac{x}{2}\right)^2-2.\dfrac{x}{2}.y+y^2\)
\(=\left(\dfrac{x^2}{2}-y\right)^2\)
b, \(x^2+x+\dfrac{1}{4}=x^2+\dfrac{1}{2}.2.x+\left(\dfrac{1}{2}\right)^2=\left(x+\dfrac{1}{2}\right)^2\)
c, \(x^2+2\sqrt{3}x+3=x^2+2\sqrt{3}x+\left(\sqrt{3}\right)^2=\left(x+\sqrt{3}\right)^2\)
d, \(4x^2-1=\left(2x-1\right)\left(2x+1\right)\)
`x^2/4-2*x/2*y+y^2`
`=(x/2-y)^2`
`x^2+x+1/4`
`=x^2+2*x*1/2+(1/2)^2`
`=(x+1/2)^2`
`x^2+2sqrt3x+3`
`=x+2xsqrt3+sqrt3^2`
`=(x+sqrt3)^2`
`4x^2-1`
`=(2x)^2-1`
`=(2x-1)(2x+1)`
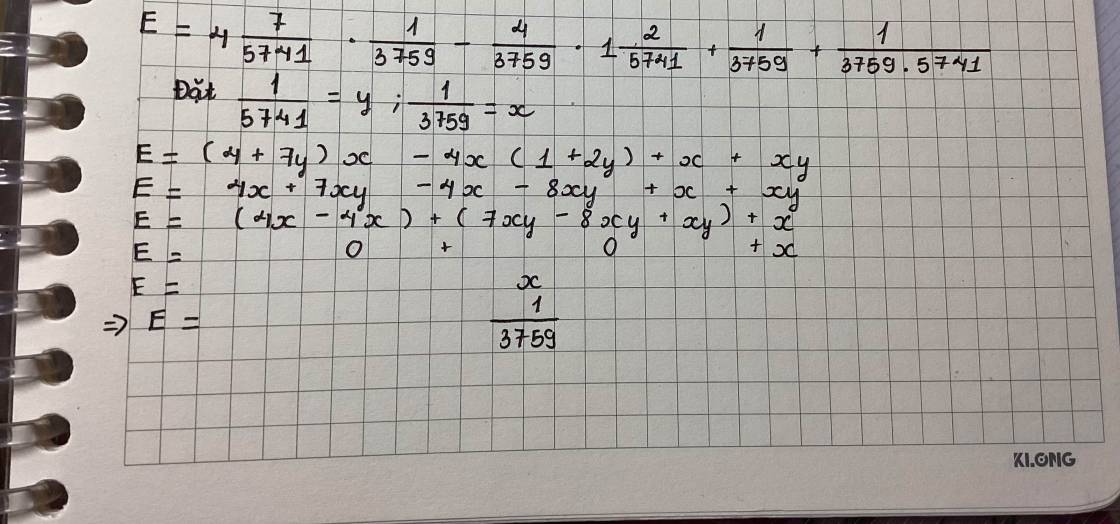
\(xy\left(x-y\right)+yz\left(y-z\right)+xz\left(z-x\right)\\ =xy\left(x-y\right)+yz\left[-\left(x-y\right)-\left(z-x\right)\right]+xz\left(z-x\right)\\ =xy\left(x-y\right)-yz\left(x-y\right)-yz\left(z-x\right)+xz\left(z-x\right)\\ =\left(x-y\right)\left(xy-yz\right)+\left(z-x\right)\left(xz-yz\right)\\ =y\left(x-y\right)\left(x-z\right)+z\left(z-x\right)\left(x-y\right)\\ =\left(x-y\right)\left(x-z\right)\left(y-z\right)\)