a) ta có : \(N=-21x^{99}-21x^{98}-...-21x^2-21x\)

\(\Rightarrow xN=-21x^{100}-21x^{99}-...-21x^2-21x^2\)

\(\Rightarrow xN-N=-21x^{100}+21x\)

\(\Leftrightarrow\left(x-1\right)N=-21x^{100}+21x\Leftrightarrow N=\dfrac{21x-21x^{100}}{x-1}\)

\(\Rightarrow A=x^{100}-21x^{99}-21x^{98}-...-21x^2-21x+2010\)

\(=x^{100}+\dfrac{21x-21x^{100}}{x-1}+2010\)

\(=\dfrac{21x-21x^{100}+x^{101}-x^{100}+2010x-2010}{x-1}\)

\(=\dfrac{x^{101}-22x^{100}+2031x-2010}{x-1}\)

thay \(x=22\) ta có : \(A=\dfrac{22^{101}-22.22^{100}+2031.22-2010}{22-1}\)

\(=\dfrac{22^{101}-22^{101}+2031.22-2010}{21}=\dfrac{2031.22-2010}{21}=2032\)

vậy ............................................................................................................

câu b lm tương tự .

a:

Sửa đề: A=x^4-9x^3+21x^2+x+a

A chia hết cho B

=>x^4-2x^3-7x^3+14x^2+7x^2-14x+15x-30+a+30 chia hết cho x-2

=>a+30=0

=>a=-30

b: A chia hết cho B

=>x^4+2x^3-12x^3-24x^2+45x^2+90x-82x-164+a+164 chia hết cho x+2

=>a+164=0

=>a=-164

chi tiết đc kh ạ?

\(a,=10x^3-5x^2+5x\\ b,=x^3+27\\ c,=\dfrac{5}{2}xy-1-\dfrac{1}{2}y\\ d,=\left(2x^3-10x^2-11x^2+55x+12x-60\right):\left(x-5\right)\\ =\left[2x^2\left(x-5\right)-11x\left(x-5\right)+12\left(x-5\right)\right]:\left(x-5\right)\\ =2x^2-11x+12\)

a: \(=10x^3-5x^2+5x\)

b: \(=x^3-27\)

b) Ta có:

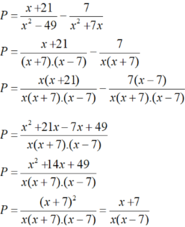
Tại x= 5 thì biểu thức P xác định nên giá trị của biểu thức P tại x = 5 là:

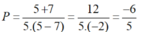
\(x^4-9x^3+21x^2+x+a=\left(x^2-8x+15\right)\left(x^2-x-2\right)+a+30\)

\(\Rightarrow a+30=0\Rightarrow a=-30\)

Bài 1: 

a: \(=2x^2-3xy+5y^2\)

b: \(=\dfrac{2x^3-10x^2-11x^2+55x+12x-60}{x-5}=2x^2-11x+12\)

c: \(=\dfrac{6x^3+3x^2-10x^2-5x+4x+2}{2x+1}=3x^2-5x+2\)

c: \(=\dfrac{\left(x+3\right)^2-y^2}{x+y+3}=x+3-y\)

a) \(\left(2x-y\right)\left(4x^2-2xy+y^2\right)\)

\(=8x^3-4x^2y+2xy^2-4xy^2+2xy^2-y^3\)

\(=8x^3-8x^2y+4xy^2-y^3\)

b) \(\left(6x^5y^2-9x^4y^3+15x^3y^4\right):3x^3y^2\)

\(=2x^2-3xy+5y^2\)

a) Điều kiện: x2 - 49 ≠ 0 và x2 + 7x ≠ 0.

Ta có: x2 - 49 = (x - 7)(x + 7); x2 + 7x = x(x + 7).

Vậy: x - 7 ≠ 0; x + 7 ≠ 0 và x ≠ 0 ⇒ x ≠ ±7 và x ≠ 0.

\(A=\dfrac{6x^2+21x+22}{x^2+4x+4}\)

\(=\dfrac{6\left(x^2+4x+4\right)-3x-2}{x^2+4x+4}\)

\(=6+\dfrac{-3x-2}{\left(x+2\right)^2}\)

\(=6+\dfrac{-3\left(x+2\right)+4}{\left(x+2\right)^2}\)

\(=6-\dfrac{3}{x+2}+\dfrac{4}{\left(x+2\right)^2}\)

-Đặt \(a=\dfrac{1}{x+2}\) thì:

\(A=6-3a+4a^2=\left(2a\right)^2-2.2a.\dfrac{3}{4}+\dfrac{9}{16}+\dfrac{87}{16}=\left(2a-\dfrac{3}{4}\right)^2+\dfrac{87}{16}\ge\dfrac{87}{16}\)

\(A_{min}=\dfrac{87}{16}\)\(\Leftrightarrow\left(2a-\dfrac{3}{4}\right)^2=0\Leftrightarrow2a-\dfrac{3}{4}=0\Leftrightarrow2a=\dfrac{3}{4}\)

\(\Leftrightarrow2.\dfrac{1}{x+2}=\dfrac{3}{4}\Leftrightarrow\dfrac{1}{x+2}=\dfrac{3}{8}\Leftrightarrow x+2=\dfrac{8}{3}\Leftrightarrow x=\dfrac{2}{3}\)

-Kết hợp phương pháp nhóm hạng tử với đặt ẩn phụ luôn.