Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
$A=2^{1+2+3+...+12}.5^{2+4+6+...+16}=2^{78}.5^{72}$
$=(2.5)^{72}.2^6=10^{72}.2^6$
Tích A có $72$ chữ số $0$.

Dãy số này có số số chia hết cho 5 là:
(0+2020):5+1=405 (số)
Dãy số này có số số chia hết cho 2 là:
(0+2020):2+1=1011 (Số)
Vì 5.2=10 tạo nên 1 số là 10 có cstc là 0
Dãy số có số chữ số tận cùng là số chữ số 0 là:
(5.5.5.5....5).(2.2.2.2...)=[(5.2)(5.2).(5.2).(5.2).(2.2.2...2)]
có 405 số 5 có 1011 chữ số 2 có 405 cặp số (5.2)
=10.10.10....10.(2.2.2..2)=> cstc của A là 405 chữ số 0


giải câu b còn câu a đề nói ko rõ ko hiểu
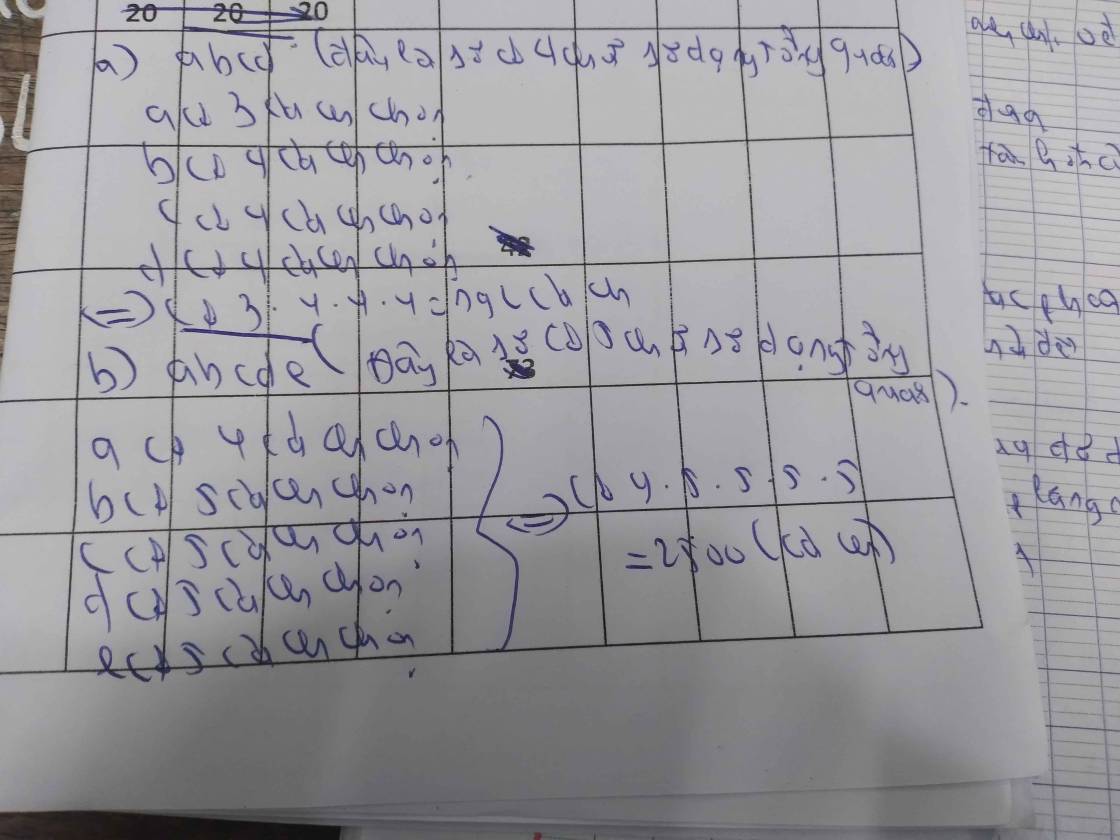
số thứ nhất có 3 cách chọn
số thứ hai có 3 cách chọn
Số thứ ba có 2 cách chọn
Số cuối cùng có 1 cách chọn
lập được số số hạng có các chữ số khác nhau là
3x3x2x1=18 số


Ban vao day nhaTích A = 1 . 2 . 3 . ... . 500 có tận cùng bằng bao nhiêu chữ số 0
Tích 500! có tận cùng là :
\(\left[\frac{500}{5}\right]+\left[\frac{500}{5^2}\right]+\left[\frac{500}{5^3}\right]=124\)(chữ số 0)