
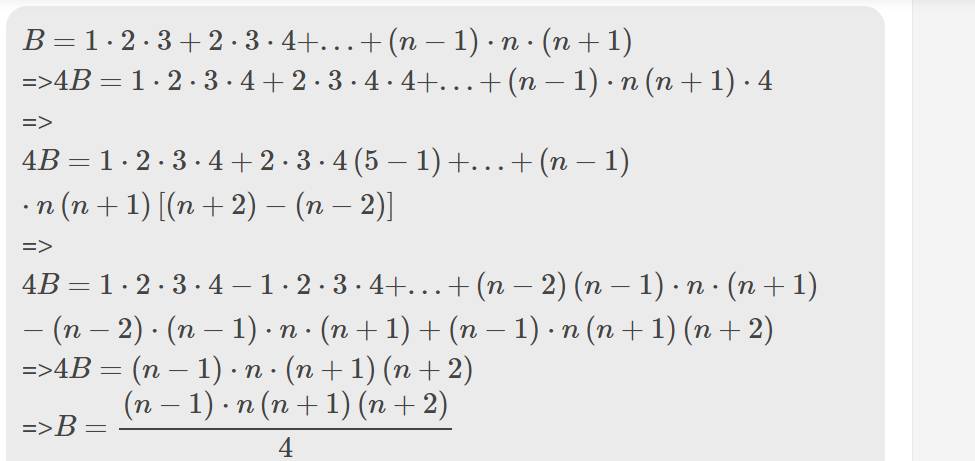
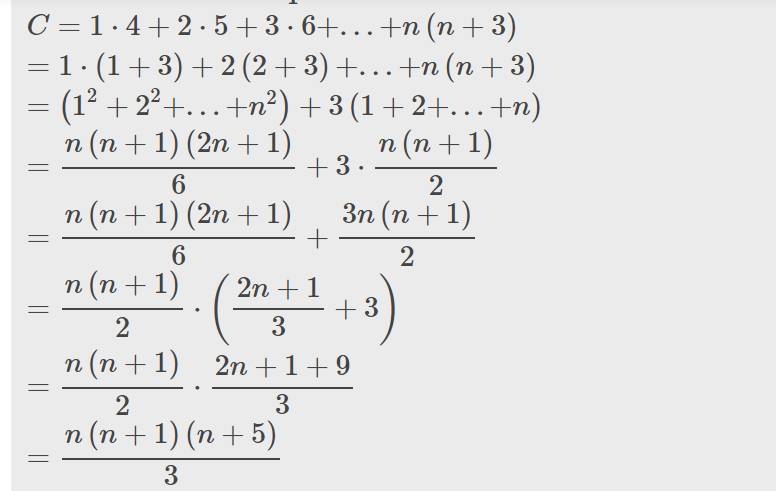

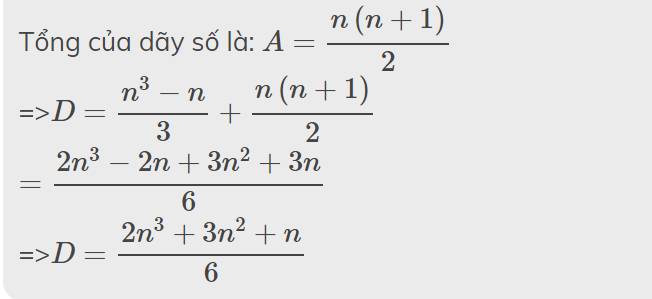
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

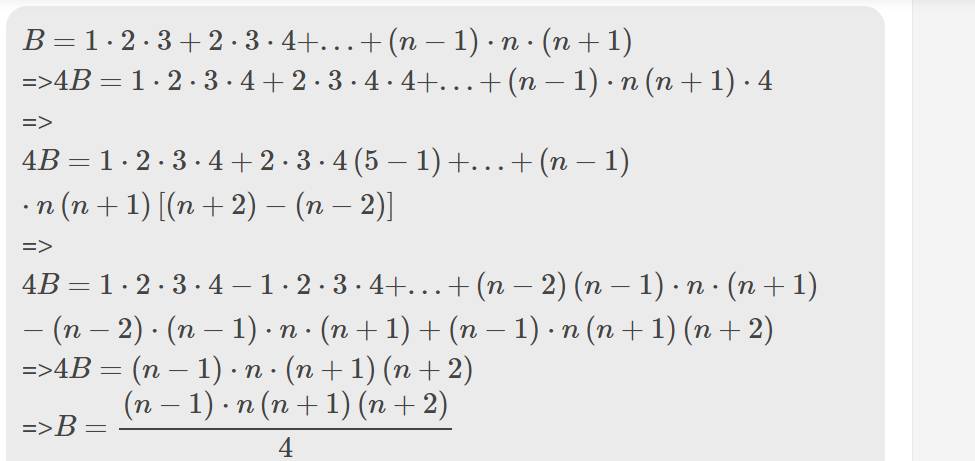
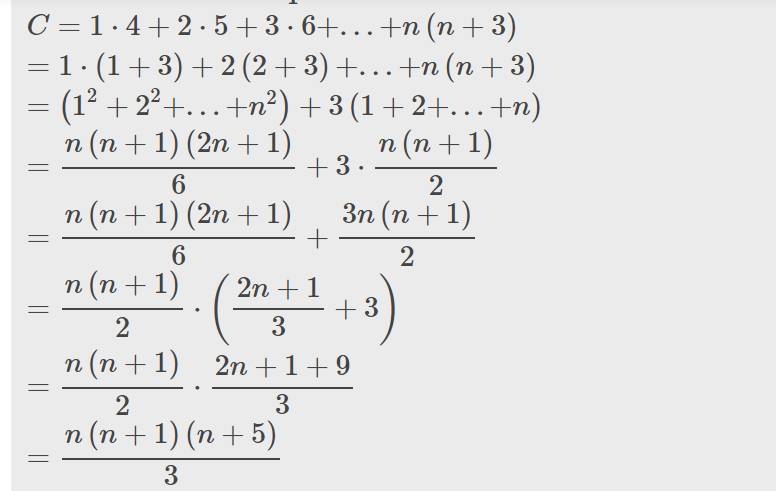

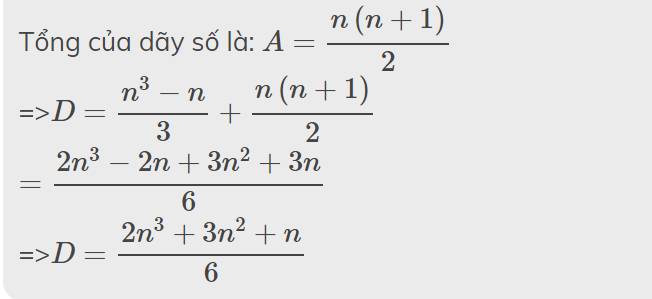

\(B=1\cdot2\cdot3+2\cdot3\cdot4+...+\left(n-1\right)\cdot n\cdot\left(n+1\right)\)
=>\(4B=1\cdot2\cdot3\cdot4+2\cdot3\cdot4\cdot4+...+\left(n-1\right)\cdot n\left(n+1\right)\cdot4\)
=>\(4B=1\cdot2\cdot3\cdot4+2\cdot3\cdot4\left(5-1\right)+...+\left(n-1\right)\cdot n\left(n+1\right)\left[\left(n+2\right)-\left(n-2\right)\right]\)
=>\(4B=1\cdot2\cdot3\cdot4-1\cdot2\cdot3\cdot4+...+\left(n-2\right)\left(n-1\right)\cdot n\cdot\left(n+1\right)-\left(n-2\right)\cdot\left(n-1\right)\cdot n\cdot\left(n+1\right)+\left(n-1\right)\cdot n\left(n+1\right)\left(n+2\right)\)
=>\(4B=\left(n-1\right)\cdot n\cdot\left(n+1\right)\left(n+2\right)\)
=>\(B=\dfrac{\left(n-1\right)\cdot n\left(n+1\right)\left(n+2\right)}{4}\)
\(C=1\cdot4+2\cdot5+3\cdot6+...+n\left(n+3\right)\)
\(=1\cdot\left(1+3\right)+2\left(2+3\right)+...+n\left(n+3\right)\)
\(=\left(1^2+2^2+...+n^2\right)+3\left(1+2+...+n\right)\)
\(=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}+3\cdot\dfrac{n\left(n+1\right)}{2}\)
\(=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}+\dfrac{3n\left(n+1\right)}{2}\)
\(=\dfrac{n\left(n+1\right)}{2}\cdot\left(\dfrac{2n+1}{3}+3\right)\)
\(=\dfrac{n\left(n+1\right)}{2}\cdot\dfrac{2n+1+9}{3}\)
\(=\dfrac{n\left(n+1\right)\left(n+5\right)}{3}\)
\(D=1^2+2^2+...+n^2\)
\(=1+\left(1+1\right)\cdot2+\left(1+2\right)\cdot3+...+\left(1+n-1\right)\cdot n\)
\(=1+2+3+...+n+\left(1\cdot2+2\cdot3+...+\left(n-1\right)\cdot n\right)\)
Đặt \(A=1+2+3+...+n;E=1\cdot2+2\cdot3+...+\left(n-1\right)\cdot n\)
\(E=1\cdot2+2\cdot3+...+\left(n-1\right)\cdot n\)
=>\(3E=1\cdot2\cdot3+2\cdot3\cdot3+...+\left(n-1\right)\cdot n\cdot3\)
=>\(3E=1\cdot2\cdot3+2\cdot3\cdot\left(4-1\right)+...+\left(n-1\right)\cdot n\left[\left(n+1\right)-\left(n-2\right)\right]\)
=>\(3E=1\cdot2\cdot3-1\cdot2\cdot3+2\cdot3\cdot4+...+\left(n-1\right)\cdot n\left(n-2\right)-\left(n-1\right)\cdot n\left(n-2\right)+\left(n-1\right)\cdot n\cdot\left(n+1\right)\)
=>\(3E=\left(n-1\right)\cdot n\left(n+1\right)=n^3-n\)
=>\(E=\dfrac{n^3-n}{3}\)
\(A=1+2+3+...+n\)
Số số hạng là n-1+1=n(số)
Tổng của dãy số là: \(A=\dfrac{n\left(n+1\right)}{2}\)
=>\(D=\dfrac{n^3-n}{3}+\dfrac{n\left(n+1\right)}{2}\)
\(=\dfrac{2n^3-2n+3n^2+3n}{6}\)
=>\(D=\dfrac{2n^3+3n^2+n}{6}\)

TK
S=1.4+2.5+3.6+4.7+....+n.(n+3) S = 1. ( 2 + 2 ) + 2. ( 3 + 2 ) + 3. ( 4 + 2 ) + . . . + n . [ ( n + 1 ) + 2 ] S = 1.2 + 2.3 + 3.4 + . . . . + n . ( n + 1 ) + ( 1.2 + 2.2 + 3.2 + . . . . + n .2 ) Đặt A = 1.2 + 2.3 + 3.4 + . . . . + n . ( n + 1 ) 3 A = 1.2.3 + 2.3. ( 4 − 1 ) + . . . . + n . ( n + 1 ) . [ ( n + 2 ) − ( n − 1 ) 3 A = 1.2.3 + 2.3.4 − 1.2.3 + . . . . + n . ( n + 1 ) . ( n + 2 ) − ( n − 1 ) . n . ( n + 1 ) 3 A = n . ( n + 1 ) . ( n + 2 ) A = [ n . ( n + 1 ) . ( n + 2 ) ] : 3 S = [ n . ( n + 1 ) . ( n + 2 ) ] : 3 + 2. ( 1 + 2 + 3 + . . . + n ) S = [ n . ( n + 1 ) . ( n + 2 ) ] : 3 + 2. n . ( n + 1 ) : 2 S = n . ( n + 1 ) . ( n + 2 ) : 3 + n . ( n + 1 ) S = n . ( n + 1 ) . [ ( n + 2 ) : 3 + 1 )
D = 1^2 + 2^2 + 3^2 + ... + n^2
= 1.( 2 - 1 ) + 2.( 3-1 ) + 3.( 4-1 ) + .... + n.[ ( n+ 1) - 1 ]
= 1.2 - 1 + 2.3 - 2 + 3.4 - 3 + .... + n.( n+1 ) - n
= [ 1.2 + 2.3 + 3.4 + ..... + n.( n + 1 ) ] - ( 1 + 2 + 3 + .... + n )
= { [ n.( n+1 ).( n+2 )] /3 } - { [ n.( n+1)] /2 }
= { n(n+1)(2n+1) }/ 6
Vậy.........

3F= 1.2.(3-0)+ 2.3.(4-1)+...+ n.(n+1).[(n+2)-(n-1)]
=[1.2.3+ 2.3.4+...+ (n-1)n(n+1)+ n(n+1)(n+2)]- [0.1.2+ 1.2.3+...+(n-1)n(n+1)]
=n(n+1)(n+2)
=>F
H=1.2.3+2.3.4+3.4.5+...+n(n+1)(n+2)
=> 4H=1.2.3(4-0)+2.3.4(5-1)+...+n(n+1)(n+2)((n+3)-(n-1))
=1.2.3.4-0.1.2.3+2.3.4.5-1.2.3.4+...+n(n+1)(n+2)(n+3)-(n-1).n(n+1)(n+2)
=n(n+1)(n+2)(n+3)

Ta thấy: 1.4 = 1.(1 + 3)
2.5 = 2.(2 + 3)
3.6 = 3.(3 + 3)
4.7 = 4.(4 + 3)
…….
n(n + 3) = n(n + 1) + 2n
Vậy C = 1.2 + 2.1 + 2.3 + 2.2 + 3.4 + 2.3 + … + n(n + 1) +2n
C = 1.2 + 2 +2.3 + 4 + 3.4 + 6 + … + n(n + 1) + 2n
C = [1.2 +2.3 +3.4 + … + n(n + 1)] + (2 + 4 + 6 + … + 2n)
⇒ 3C = 3.[1.2 +2.3 +3.4 + … + n(n + 1)] + 3.(2 + 4 + 6 + … + 2n)
3C = 1.2.3 + 2.3.3 + 3.4.3 + … + n(n + 1).3 + 3.(2 + 4 + 6 + … + 2n)
3C = n(n + 1)(n + 2) +
⇒ C = +
=

Ta thấy: 1.4 = 1.(1 + 3)
2.5 = 2.(2 + 3)
3.6 = 3.(3 + 3)
4.7 = 4.(4 + 3)
…….
n(n + 3) = n(n + 1) + 2n
Vậy C = 1.2 + 2.1 + 2.3 + 2.2 + 3.4 + 2.3 + … + n(n + 1) +2n
C = 1.2 + 2 +2.3 + 4 + 3.4 + 6 + … + n(n + 1) + 2n
C = [1.2 +2.3 +3.4 + … + n(n + 1)] + (2 + 4 + 6 + … + 2n)
⇒ 3C = 3.[1.2 +2.3 +3.4 + … + n(n + 1)] + 3.(2 + 4 + 6 + … + 2n)
3C = 1.2.3 + 2.3.3 + 3.4.3 + … + n(n + 1).3 + 3.(2 + 4 + 6 + … + 2n)
3C = n(n + 1)(n + 2) +
⇒ C = +
=

\(A=1\cdot4+2\cdot5+3\cdot6+...+n\left(n+3\right)\)
\(=1\left(1+3\right)+2\left(2+3\right)+3\left(3+3\right)+...+n\left(n+3\right)\)
\(=\left(1^2+2^2+...+n^2\right)+3\left(1+2+3+...+n\right)\)
\(=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}+3\cdot\dfrac{n\left(n+1\right)}{2}\)
\(=\dfrac{n\left(n+1\right)\left(2n+1\right)+9n\left(n+1\right)}{6}\)
\(=\dfrac{n\left(n+1\right)\left(2n+1+9\right)}{6}\)
\(=\dfrac{n\left(n+1\right)\left(2n+10\right)}{6}=\dfrac{n\left(n+1\right)\left(n+5\right)}{3}\)
