
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 4:
\(a,\sin B=\dfrac{AC}{BC}=\dfrac{12}{13};\cos B=\dfrac{AB}{BC}=\dfrac{5}{13};\tan B=\dfrac{AC}{AB}=\dfrac{12}{5};\cot B=\dfrac{AB}{AC}=\dfrac{5}{12}\\ b,\text{Áp dụng HTL: }\left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=\dfrac{60}{13}\left(cm\right)\\BH=\dfrac{AB^2}{BC}=\dfrac{25}{13}\left(cm\right)\end{matrix}\right.\\ \sin B=\dfrac{12}{13}\approx67^0\\ \Rightarrow\widehat{B}\approx67^0\\ \Rightarrow\widehat{HAB}=90^0-\widehat{B}\approx23^0\)


a.
Áp dụng hệ thức lượt trong tam giác vuông ta có:
$\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}$
$\Leftrightarrow \frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AB^2}=\frac{1}{3a^2}$
$\Rightarrow AC=\sqrt{3}a$
$BC=\sqrt{AB^2+AC^2}=\sqrt{a^2+3a^2}=2a$
b.
$HB=\frac{BC}{4}$ thì $HC=\frac{3}{4}BC$
$\Rightarrow \frac{HB}{HC}=\frac{1}{3}$
Áp dụng hệ thức lượt trong tam giác vuông:
$AB^2=BH.BC; AC^2=CH.BC$
$\Rightarrow \frac{AB}{AC}=\sqrt{\frac{BH}{CH}}=\frac{\sqrt{3}}{3}$
Áp dụng định lý Pitago:
$4a^2=BC^2=AB^2+AC^2=(\frac{\sqrt{3}}{3}.AC)^2+AC^2$
$\Rightarrow AC=\sqrt{3}a$
$\Rightarrow AB=a$
c.
Áp dụng hệ thức lượt trong tam giác vuông:
$AB^2=BH.BC$
$\Leftrightarrow AB^2=BH(BH+CH)$
$\Leftrightarrow a^2=BH(BH+\frac{3}{2}a)$
$\Leftrightarrow BH^2+\frac{3}{2}aBH-a^2=0$
$\Leftrightarrow (BH-\frac{a}{2})(BH+2a)=0$
$\Rightarrow BH=\frac{a}{2}$
$BC=BH+CH=2a$
$AC=\sqrt{BC^2-AB^2}=\sqrt{3}a$
d. Tương tự phần a.

áp dụng định lí pitago trong tam giác vuông ABC ( A = 90 )
\(AB^2+AC^2=BC^2\Rightarrow BC=10\)
áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ABC co
\(AB\times AC=AH\times BC\Rightarrow AH=4.8\)
\(AB^2=BH\times BC\Rightarrow BH=3.6\)
\(HC=10-3.6=6.4\)
cho tam giác ABC vuông tại A có AC = 8cm , BH= 4cm . Dường cao AH . 1) tính các cạnh , gốc còn lại !

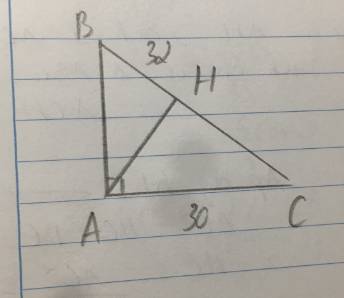

đề còn cho j ko vậy
ko ạ cứu mik zới