1. Vì tứ giác ABCD là hình thang AB//CD nên góc A+ góc D=180 độ mà góc A- góc D=40 do suy ra goc D= (180-40):2=70 do suy ra goc A= 180-70=110 do

Tương tự ta cũng có: \(\widehat{B}+\widehat{C}=180^0\)ma \(\widehat{B}=4\times\widehat{C}\)\(\Rightarrow4\times\widehat{C}+\widehat{C}=180^0\Rightarrow5\times\widehat{C}=180^0\Rightarrow\widehat{C}=36^0\Rightarrow\widehat{B}=180^0-36^0=144^0\)

Còn bài 2 thì tớ chưa nghĩ ra bạn rang đoi nhá

2. Vì AB//DC ma \(K\in AB\Rightarrow\widehat{AKD}=\widehat{KDC};\widehat{BKC}=\widehat{KCD}\) (1)

    Vì DK là tia phân giác của \(\widehat{ADC}\Rightarrow\widehat{ADK}=\widehat{KDC}\)và CK là tia phân giác của \(\widehat{BCD}\Rightarrow\widehat{KCB}=\widehat{KCD}\)(2)

Từ(1) vả (2) ta có: \(\widehat{AKD}=\widehat{ADK};\widehat{BKC}=\widehat{BCK}\)suy ra tam giác AKD cân tại A và tam giác KBC cân tại B 

\(\Rightarrow AK=AD;BK=BC\Rightarrow AK+BK=AD+BC\Rightarrow AB=AD+BC\)

Ta có a//b nên suy ra a1=a2=b1=b2(so le trong và đồng vị)

a3=a4=b3=b4 ( so le trong và đồng vị)

Mà góc lớn nhất gấp 3 lần góc bé nhất nên góc bé nhất có số đo là 180/4=45 độ

góc lớn nhất có số đo là 3*45= 135 độ

chúc bạn học tốt

Hồi qua đăng rồi mà

Ta có

\(\widehat{A1}=\widehat{A3}=\widehat{B1}=\widehat{B4}\)

( vì là các góc đồng vị ; so le trong ; đối đỉnh )

\(\widehat{A2}=\widehat{A2}=\widehat{B2}=\widehat{B3}\)

( vì là các góc đồng vị ; so le trong ; đối đỉnh )

Giải sử các\(\widehat{A2}=\widehat{A2}=\widehat{B2}=\widehat{B3}\)>\(\widehat{A1}=\widehat{A3}=\widehat{B1}=\widehat{B4}\)

\(\Rightarrow\widehat{A2}=3.\widehat{A1}\)

Mà \(\widehat{A2}+\widehat{A1}=\)180⁰

=>\(3.\widehat{A1}+\widehat{A1}=180^0\)

\(\Rightarrow4.\widehat{A1}=180^0\)

\(\Rightarrow\widehat{A1}=45^0\)

\(\Rightarrow\widehat{A2}=135^0\)

Vậy \(\widehat{A2}=\widehat{A2}=\widehat{B2}=\widehat{B3}=135^0\)

\(\widehat{A1}=\widehat{A3}=\widehat{B1}=\widehat{B4}=45^0\)

bn Silver bullet ơi , bn có thể nêu rõ các góc nào đồng vị , các góc nào so le trong và đối đỉnh không bn ? 

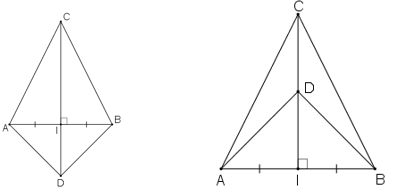
Xét tam giác ACI và tam giác BCI , có

CI là cạnh chung

AC = BC

AI= BI

=> tam giác ACI = tam giác BCI

Xét tam giác ACD và tam giác BCD , có

CD là cạnh chung

AD = BD

AC =BC

=> tam giác ACD = tam giác BCD

Xét tam giác ADI và tam giác BDI , có

DI là cạnh chung

AD = BD

AI = BI

=> tam giác ADI = tam giác BDI

ok 3 cặp nha thư

Có hai trường hợp:

   + ΔAIC = ΔBIC (c.g.c) vì:

AI = IB (gt)

∠AIC = ∠BIC = 90o

CI chung.

   + ΔAID = ΔBID(c.g.c) vì:

AI = ID (gt)

∠AID = ∠BID = 90o

DI chung.

   + ΔACD = ΔBCD(c.c.c) vì:

AC = BC (Lấy từ ΔAIC = ΔBIC)

AD = BD (Lấy từ ΔAID = ΔBID)

CD chung