Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1) Ta có: S = BH x (BC + DA) : 2
+ BCKH là hình chữ nhật nên BC = KH = x
+ BH = x
+ AD = AH + HK + KD = 7 + x + 4 = 11 + x.
Vậy S = BH x (BC + DA) : 2 = x.(x + 11 + x) : 2 = x.(2x + 11) : 2.
2) S = SABH + SBCKH + SCKD
+ ABH là tam giác vuông tại H
⇒ SBAH = 1/2.BH.AH = 1/2.7.x = 7x/2.
+ BCKH là hình chữ nhật
⇒ SBCKH = x.x = x2.
+ CKD là tam giác vuông tại K
⇒ SCKD = 1/2.CK.KD = 1/2.4.x = 2x.
Do đó: S = SABH + SBCKH + SCKD = 7x/2 + x2 + 2x = x2 + 11x/2.
- Với S = 20 ta có phương trình:
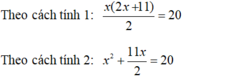
Hai phương trình trên tương đương với nhau. Và cả hai phương trình trên đều không phải là phương trình bậc nhất.
Ta có: S = SABH + SBCKH + SCKD.
= 1212.AH.BH + BH.HK + 1212CK.KD
= 1212.7x + x.x + 1212x.4
= 7272x + x2 + 2x
Vậy S = 20 ta có hai phương trình:
x(11+2x)2x(11+2x)2 = 20 (1)
7272x + x2 + 2x = 20 (2)
Cả hai phương trình không có phương trình nào là phương trình bậc nhất.
1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực
1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực
![[CHUẨN NHẤT] Thế nào là hai phương trình tương đương](https://api.toploigiai.vn/storage/uploads/the-nao-la-hai-phuong-trinh-tuong-duong_1)
![[CHUẨN NHẤT] Thế nào là hai phương trình tương đương (ảnh 2)](https://api.toploigiai.vn/storage/uploads/the-nao-la-hai-phuong-trinh-tuong-duong_2)
a) Phương trình bậc nhất một ẩn là phương trình 2x -8 = 0
b) Hai phương trình tương đương là hai phương trình có cùng tập nghiệm
Hai PT đã cho tương đương với nhau vì chúng có cùng tập nghiệm
S = {-2/3}
a) Phương trình bậc nhất một ẩn là phương trình :
2x - 8 = 0
b) Hai phương trình tương đương với nhau vì chúng có cùng tập nghiệm
Hai PT đã cho tương đương với nhau vì chúng có cùng tập nghiệm
S = ( -2 / 3 )
ai tk mk mk tk lại!!
Câu 1:
Ta thấy \(S_2=\dfrac{\sqrt{3}+S_1}{1-\sqrt{3}S_1}=\dfrac{\sqrt{3}+1}{1-\sqrt{3}}=\dfrac{\left(1+\sqrt{3}\right)^2}{\left(1-\sqrt{3}\right)\left(1+\sqrt{3}\right)}\)\(=\dfrac{4+2\sqrt{3}}{-2}=-2-\sqrt{3}\)
Từ đó \(S_3=\dfrac{\sqrt{3}+S_2}{1-\sqrt{3}S_2}=\dfrac{\sqrt{3}-2-\sqrt{3}}{1-\sqrt{3}\left(-2-\sqrt{3}\right)}=\dfrac{-2}{4+2\sqrt{3}}=\dfrac{1}{-2-\sqrt{3}}\)
và \(S_4=\dfrac{\sqrt{3}+S_3}{1-\sqrt{3}S_3}=\dfrac{\sqrt{3}+\dfrac{1}{-2-\sqrt{3}}}{1-\dfrac{\sqrt{3}}{-2-\sqrt{3}}}=\dfrac{-2\sqrt{3}-3+1}{-2-\sqrt{3}-\sqrt{3}}=1\)
Đến đây ta thấy \(S_4=S_1\). Cứ tiếp tục làm như trên, ta rút ra được:
\(S_{3k+1}=1\); \(S_{3k+2}=-2-\sqrt{3}\) và \(S_{3k+3}=\dfrac{1}{-2-\sqrt{3}}\), với \(k\inℕ\)
Ta tính số các số thuộc mỗi dạng \(S_{3k+i}\left(i=1,2,3\right)\) từ \(S_1\) đến \(S_{2017}\).
- Số các số hạng có dạng \(S_{3k+1}\) là \(\left(2017-1\right):3+1=673\) số
- Số các số hạng có dạng \(S_{3k+2}\) là \(\left(2015-2\right):3+1=672\) số
- Số các số hạng có dạng \(S_{3k+3}\) là \(\left(2016-3\right):3+1=672\) số
Như thế, tổng S có thể được viết lại thành
\(S=\left(S_1+S_4+...+S_{2017}\right)+\left(S_2+S_5+...+S_{2015}\right)+\left(S_3+S_6+...+S_{2016}\right)\)
\(S=613+612\left(-2-\sqrt{3}\right)+612\left(\dfrac{1}{-2-\sqrt{3}}\right)\)
Tới đây mình lười rút gọn lắm, nhưng ý tưởng làm bài này là như vậy.
Có \(\left(x-\sqrt{x^2+5}\right).\left(y-\sqrt{y^2+5}\right)=5\) (1)
\(\Leftrightarrow\dfrac{\left(x-\sqrt{x^2+5}\right).\left(x+\sqrt{x^2+5}\right)}{x+\sqrt{x^2+5}}.\dfrac{\left(y-\sqrt{y^2+5}\right).\left(y+\sqrt{y^2+5}\right)}{y+\sqrt{y^2+5}}=5\)
\(\Leftrightarrow\left(x+\sqrt{x^2+5}\right).\left(y+\sqrt{y^2+5}\right)=5\) (2)
Từ (1) và (2) ta có \(\left(x-\sqrt{x^2+5}\right).\left(y-\sqrt{y^2+5}\right)=\left(x+\sqrt{x^2+5}\right).\left(y+\sqrt{y^2+5}\right)\)
\(\Leftrightarrow x\sqrt{y^2+5}+y\sqrt{x^2+5}=0\)
\(\Leftrightarrow x^2\left(y^2+5\right)=y^2\left(x^2+5\right)\left(y\le0;x\ge0\right)\)
\(\Leftrightarrow x^2-y^2=0\Leftrightarrow\left[{}\begin{matrix}x=y\left(\text{loại}\right)\\x=-y\left(\text{nhận}\right)\end{matrix}\right.\)
Khi đó M = x3 + y3 = 0
N = x2 + y2 = 2y2
a.
(1) là pt bậc nhất 1 ẩn khi và chỉ khi \(2\left(m-1\right)\ne0\Leftrightarrow m\ne1\)
b.
Ta có: \(2x+5=3\left(x+2\right)-1\)
\(\Leftrightarrow2x+5=3x+5\)
\(\Leftrightarrow x=0\)
Do đó (1) tương đương (*) khi (1) nhận \(x=0\) là nghiệm
\(\Rightarrow2\left(m-1\right).0+3=2m-5\)
\(\Rightarrow m=4\)
Hướng dẫn giải:
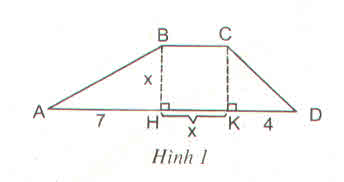
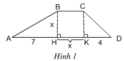
Gọi S là diện tích hình thang ABCD.
1) Theo công thức
S = BH(BC+DA)2BH(BC+DA)2
Ta có: AD = AH + HK + KD
=> AD = 7 + x + 4 = 11 + x
Do đó: S = x(11+2x)2x(11+2x)2
2) Ta có: S = SABH + SBCKH + SCKD.
= 1212.AH.BH + BH.HK + 1212CK.KD
= 1212.7x + x.x + 1212x.4
= 7272x + x2 + 2x
Vậy S = 20 ta có hai phương trình:
x(11+2x)2x(11+2x)2 = 20 (1)
7272x + x2 + 2x = 20 (2)
Cả hai phương trình không có phương trình nào là phương trình bậc nhất.
a) theo cách tính thứ nhất, diện tích hình thang là :
SABCD= BH.(BC+AD):2= x(x+7+x+4):2
=x(2x+11):2 = \(\dfrac{1}{2}\)x(2x+11) (đvdt) (1)
b) theo cách tính thứ hai
SABCD=SAHB+SCKD= \(\dfrac{1}{2}\).7x+x2+\(\dfrac{1}{2}\).4x
=\(\dfrac{7x+2x^2+4x}{2}\)= \(\dfrac{2x^2+11x}{2}\) (đvdt) (2)
Với S = 20 thì (1) và (2) trở thành x2+5,5x =20 thì đây là một phương trình bậc hai (vì có x2).
Vậy trong hai phương trình trên không có phương trình nào là phương trình bậc nhất.