Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(A=3\left(x+5\right)+x^2\)
Thay x = 1 vào A, ta được:
\(A=3\left(1+5\right)+1^2\)
\(A=3.6+1\)
\(A=19\)
b) \(B=3x\left(x+2\right)-x\left(x+1\right)\)
Thay x = -1 vào B, ta được:
\(B=3.\left(-1\right)\left(-1+2\right)-\left(-1\right)\left(-1+1\right)\)
\(B=-3-0\)
\(B=-3\)
c) \(C=7x\left(x-5\right)+3\left(x-2\right)\)
Thay x = 0 vào C, ta được:
\(C=7.0.\left(0-5\right)+3.\left(0-2\right)\)
\(C=0+3.\left(-2\right)\)
\(C=-6\)
d) \(D=-2x\left(x+1\right)+4\left(x+2\right)\)
Thay x = -1 vào D, ta được:
\(D=-2\left(-1\right)\left(-1+1\right)+4\left(-1+2\right)\)
\(D=0+4\)
\(D=4\)
e) \(E=x^2-x+2x\left(x+3\right)\)
Thay x = 2 vào E, ta được:
\(E=2^2-2+2.2\left(2+3\right)\)
\(E=4-2+4.5\)
\(E=22\)
f) \(F=5-4x\left(x-2\right)\)
Thay x = -1 vào F, ta được:
\(F=5-4.\left(-1\right)\left(-1-2\right)\)
\(F=5-12\)
\(F=-7\)
g) \(G=x\left(x-5\right)-2x\left(x+1\right)+x^2\)
Thay x = -2 vào G, ta được:
\(G=-2\left(-2-5\right)-2.\left(-2\right)\left(-2+1\right)+\left(-2\right)^2\)
\(G=14-4+4\)
\(G=14\)
h) \(H=x\left(7x+2\right)-5x\left(x+3\right)\)
Thay x = 1 vào H, ta được:
\(H=1\left(7.1+2\right)-5.1\left(1+3\right)\)
\(H=9-20\)
\(H=-11\)
i) \(I=3x^2-2x\left(x-5\right)+x\left(x-7\right)\)
Thay x = 10 vào I, ta được:
\(I=3.10^2-2.10\left(10-5\right)+10.\left(10-7\right)\)
\(I=300-100+30\)
\(I=230\)

Giải:
a) \(B=3x\left(x+2\right)-x\left(x+1\right)\)
Tại x = -1, ta được:
\(B=3\left(-1\right)\left(-1+2\right)-\left(-1\right)\left(-1+1\right)\)
\(\Leftrightarrow B=-3-0=-3\)
b) \(C=7x\left(x-5\right)+3\left(x-2\right)\)
Tại x = 0, ta được:
\(C=7.0\left(0-5\right)+3\left(0-2\right)\)
\(\Leftrightarrow C=0+\left(-6\right)=-6\)
c) \(D=-2x\left(x+1\right)+4\left(x+2\right)\)
Tại x = -1, ta được:
\(D=-2\left(-1\right)\left(-1+1\right)+4\left(-1+2\right)\)
\(\Leftrightarrow D=0+4=4\)
d) \(E=x\left(x-5\right)-2x\left(x+1\right)+x^2\)
Tại x = -2, ta được:
\(E=-2\left(-2-5\right)-2\left(-2\right)\left(-2+1\right)+\left(-2\right)^2\)
\(\Leftrightarrow E=14-4+4=14\)
e) \(F=x\left(7x+2\right)-5x\left(x+3\right)\)
Tại x = 1, ta được:
\(F=1\left(7.1+2\right)-5.1\left(1+3\right)\)
\(F=9-20=-11\)
Vậy ...
\(B=3x\left(x+2\right)-x\left(x+1\right)\)
\(B=3x^2+6x-x^2-x\)
\(B=2x^2+5x\)
\(B=x\left(2x+5\right)\)
Tại x = -1 ta có :
\(B=\left(-1\right)\left[2.\left(-1\right)+5\right]=\left(-1\right).3=-3\)
\(C=7x\left(x-5\right)+3\left(x-2\right)\)
\(C=7x^2-35x+3x-6\)
\(C=7x^2-32x-6\)
Tại x=0 ta có :
\(C=7.0-32.0+6=6\)
\(D=-2x\left(x+1\right)+4\left(x+2\right)\)
\(D=-2x^2-2x+4x+8\)
\(D=-2x^2+2x+8\)
\(D=-2\left(x^2-x-4\right)\)
Tại x = -1 ta có :
\(D=-2.\left[\left(-1\right)^2-\left(-1\right)-4\right]=4\)
\(E=x\left(x-5\right)-2x\left(x+1\right)+x^2\)
\(E=x^2-5x-2x^2-2x+x^2\)
\(E=-7x\)
Tại x = -2 ta có :
\(E=-7\left(-2\right)=14\)
\(F=x\left(7x+2\right)-5x\left(x+3\right)\)
\(F=7x^2+2x-5x^2-15x\)
\(F=2x^2-13x=x\left(2x-13\right)\)
Tại x= 1 ta có :
\(F=1.\left(2.1-13\right)=-11\)

`a,4x-10=0 `
`<=> 4x=10`
`<=>x=10/4`
`<=>x=5/2`
`b, 7-3x=9-x `
`<=>-3x+x=9-7`
`<=>-2x=2`
`<=>x=-1`
`c, 2x-(3-5x) = 4(x+3)`
`<=>2x-3+5x=4x+12`
`<=>2x+5x-4x=12+3`
`<=>3x=15`
`<=>x=5`
`d, 5-(6-x)=4(3-2x) `
`<=>5-6+x=12-8x`
`<=>x+8x=12-5+6`
`<=>9x=13`
`<=>x=13/9`
`e, 4(x+3)=-7x+17 `
`<=>4x+12=-7x+17`
`<=>4x+7x=17-12`
`<=>11x=5`
`<=>x=5/11`
`f, 5(x-3) - 4=2(x-1)+7`
`<=>5x-15-4=2x-2+7`
`<=>5x-2x=15+4-2+7`
`<=>3x=24`
`<=>x=8`
`g, 5(x-3)-4=2(x-1)+7 `
`<=>5x-15-4=2x-2+7`
`<=>5x-2x=15+4-2+7`
`<=>3x=24`
`<=>x=8`
`h,4(3x-2)-3(x-4)=7x+20`
`<=>12x-8-3x+12=7x+20`
`<=>12x-3x-7x=20+8+12`
`<=>2x=40`
`<=>x=20`

b) Ta có: \(B=5x\left(x-4y\right)-4y\left(y-5x\right)\)
\(=5x^2-20xy-4y^2+20xy\)
\(=5x^2-4y^2\)
\(=5\cdot\left(-\dfrac{1}{5}\right)^2-4\cdot\left(-\dfrac{1}{2}\right)^2\)
\(=5\cdot\dfrac{1}{25}-4\cdot\dfrac{1}{4}\)
\(=\dfrac{1}{5}-1=\dfrac{-4}{5}\)

a: Ta có: x=31
nên x-1=30
Ta có: \(A=x^3-30x^2-31x+1\)
\(=x^3-x^2\left(x-1\right)-x^2+1\)
\(=x^3-x^3+x^2-x^2+1\)
=1
c: Ta có: x=16
nên x+1=17
Ta có: \(C=x^4-17x^3+17x^2-17x+20\)
\(=x^4-x^3\left(x+1\right)+x^2\left(x+1\right)-x\left(x+1\right)+20\)
\(=x^4-x^4-x^3+x^3+x^2-x^2-x+20\)
\(=20-x=4\)
d: Ta có: x=12
nên x+1=13
Ta có: \(D=x^{10}-13x^9+13x^8-13x^7+...+13x^2-13x+10\)
\(=x^{10}-x^9\left(x+1\right)+x^8\left(x+1\right)-x^7\left(x+1\right)+...+x^2\left(x+1\right)-x\left(x+1\right)+10\)
\(=10-x\)
=-2

d: Ta có: x=12
nên x+1=13
Ta có: \(D=x^{10}-13x^9+13x^8-13x^7+...+13x^2-13x+10\)
\(=x^{10}-x^9\left(x+1\right)+x^8\left(x+1\right)-x^7\left(x+1\right)+...+x^2\left(x+1\right)-x\left(x+1\right)+10\)
\(=x^{10}-x^{10}-x^9+x^9+x^8-x^8-x^7+...+x^3+x^2-x^2-x+1+9\)
\(=-x+10=-2\)
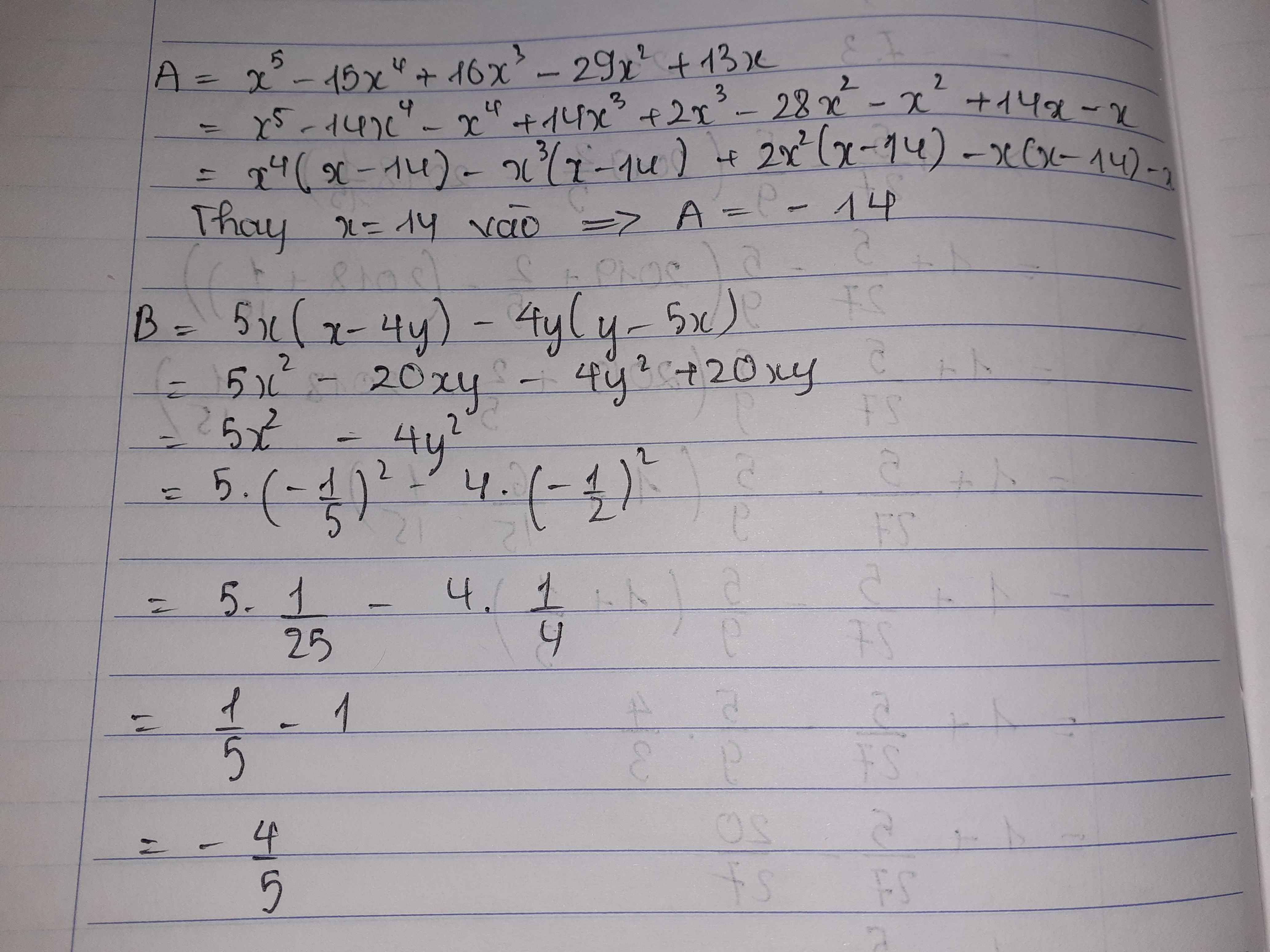
Cứ thay vào rùi thính thui
Mấy bài kia phá tung tóe rồi rút gọn hết sức xong thay x vào, làm câu c thôi nhé:
c) \(C=x^{14}-10x^{13}+10x^{12}-10x^{11}+...+10x^2-10x+10\)
riêng câu này ta thay x = 9 vào luôn, vậy ta có:
\(C=9^{14}-10\cdot9^{13}+10\cdot9^{12}-10\cdot9^{11}+...+10\cdot9^2-10\cdot9+10\)
\(=9^{14}-\left(9+1\right)\cdot9^{13}+\left(9+1\right)\cdot9^{12}-\left(9+1\right)\cdot9^{11}+...+\left(9+1\right)\cdot9^2-\left(9+1\right)\cdot9+10\)
\(=9^{14}-9^{14}-9^{13}+9^{13}+9^{12}-9^{12}-9^{11}+...+9^3+9^2-9^2-9+10\)
\(=-9+10\)
\(=1\)