Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(S_{HKE}=S_{ABC}-S_{AKE}-S_{BHE}-S_{CHK}\)
\(\Leftrightarrow\dfrac{S_{HKE}}{S_{ABC}}=1-\dfrac{S_{AKE}}{S_{ABC}}-\dfrac{S_{BHE}}{S_{ABC}}-\dfrac{S_{CHK}}{S_{ABC}}\)
\(\Leftrightarrow\dfrac{1}{4}=1-\dfrac{\dfrac{1}{2}AE.AK.sinA}{\dfrac{1}{2}AB.AC.sinA}-\dfrac{\dfrac{1}{2}BH.BE.sinB}{\dfrac{1}{2}AB.BC.sinB}-\dfrac{\dfrac{1}{2}CH.CK.sinC}{\dfrac{1}{2}AC.BC.sinC}\)
\(\Leftrightarrow\dfrac{AE.AK}{AB.AC}+\dfrac{BH.BE}{AB.BC}+\dfrac{CH.CK}{AC.BC}=\dfrac{3}{4}\)
(Để ý rằng \(\dfrac{AE}{AC}=cosA\) do tam giác ACE vuông tại E và tương tự...)
\(\Leftrightarrow cosA.cosA+cosB.cosB+cosC.cosC=\dfrac{3}{4}\)
\(\Leftrightarrow cos^2A+cos^2B+cos^2C=\dfrac{3}{4}\)
\(\Leftrightarrow1-sin^2A+1-sin^2B+1-sin^2C=\dfrac{3}{4}\)
\(\Leftrightarrow sin^2A+sin^2B+sin^2C=\dfrac{9}{4}\)

Chọn C.
Từ giả thiết ta suy ra:
B = tan2x (sin2x - 1) + sin2 x = -tan2x.cos2x + sin2x
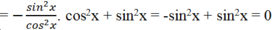

\(P.sina=\dfrac{sina}{sin2a.sina}+\dfrac{sina}{sin3a.sin2a}+...+\dfrac{sina}{sin\left(n+1\right)a.sinna}\)
\(=\dfrac{sin\left(2a-a\right)}{sin2a.sina}+\dfrac{sin\left(3a-2a\right)}{sin3a.sin2a}+...+\dfrac{sin\left[\left(n+1\right)a-na\right]}{sin\left(n+1\right)a.sinna}\)
\(=\dfrac{sin2a.cosa-cos2a.sina}{sin2a.sina}+\dfrac{sin3a.cos2a-cos3a.sin2a}{sin3a.sin2a}+\dfrac{sin\left(n+1\right)a.cosna-cos\left(n+1\right)a.sinna}{sin\left(n+1\right)a.sinna}\)
\(=cota-cot2a+cot2a-cot3a+...+cot\left(na\right)-cot\left(n+1\right)a\)
\(=cota-cot\left(n+1\right)a\)
\(\Rightarrow P=\dfrac{cota-cot\left(n+1\right)a}{sina}\)

Lần sau bạn vào cái hình E để gửi câu hỏi nha!
\(P=\dfrac{sin^2\alpha-sin\alpha\cdot cos\alpha+2cos^2\alpha}{2sin^2\alpha-cos^2\alpha}\)
\(P=\dfrac{tan^2\alpha-tan\alpha+2}{2tan^2\alpha-1}\) (Chia cả tử và mẫu cho \(cos^2\alpha\))
\(P=\dfrac{3^2-3+2}{2\cdot3^2-1}=\dfrac{8}{17}\)
Chúc bn học tốt!

\(\dfrac{1+cos2a-sin2a}{1+cos2a+sin2a}=\dfrac{2cos^2a-2sina.cosa}{2cos^2a+2sinacosa}\)
\(=\dfrac{2cosa\left(cosa-sina\right)}{2cosa\left(cosa+sina\right)}=\dfrac{cosa-sina}{cosa+sina}=\dfrac{\sqrt{2}sin\left(\dfrac{\pi}{4}-a\right)}{\sqrt{2}cos\left(\dfrac{\pi}{4}-a\right)}=tan\left(\dfrac{\pi}{4}-a\right)\)
\(\dfrac{1+cos2a-cosa}{sin2a-sina}=\dfrac{2cos^2a-cosa}{2sina.cosa-sina}=\dfrac{cosa\left(2cosa-1\right)}{sina\left(2cosa-1\right)}=\dfrac{cosa}{sina}=cota\)

Chọn A.
Sử dụng công thức hạ bậc và biến đổi tổng thành tích ta có :
A = sin2(a + b) – sin2a - sin2b
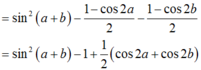
= -cos2(a + b) + cos( a + b) cos(a - b)
= cos (a +b) [ cos( a - b) – cos(a + b) ]
= 2 sina. sinb.cos(a + b)

Chọn D.
Ta có: A = sin2(a + b) –sin2a - sin2b
= ( sina.cosb + cosa.sinb) 2 - sin2a - sin2b
= sin2a.cos2b + 2sina.cosb.cosa.sinb + cos2a.sin2b - sin 2a - sin2b
= sin2a( cos2b - 1) + sin2b( cos2a - 1) + 2.sina.cosa.sinb.cosb
= - sin2a.sin2b - sin2b.sin2a + 2.sina.cosa.sinb.cosb
= 2sina.sinb( cosa.cosb - sina.sinb) = 2.sina.sinb.cos( a + b).

\(Q=sin^20^0+sin^21^0+...+sin^245^0+cos^244^0+...+cos^20^0\)
\(=\left(sin^20^0+cos^20^0\right)+\left(sin^21^0+cos^21^0\right)+...+\left(sin^244^0+cos^244^0\right)+sin^245^0\)
\(=1+1+...+1+\left(\dfrac{\sqrt{2}}{2}\right)^2\)
\(=45+\dfrac{1}{2}=\dfrac{91}{2}\)