Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : 1,12(32) = 1,12 + 0,0032
Mà 0,0032 = 32/9990
Nên : 1,12(32) = 28/25 + 32/9990 = 556/495
Nhập vào máy : Sích mak
công thức (2n - 1) ( 2n + 1) x chạy từ 1 đến 15 ok

a: ĐKXĐ: x>0
Để A là số nguyên thì \(7⋮\sqrt{x}\)
=>\(\sqrt{x}\in\left\{1;7\right\}\)
=>\(x\in\left\{1;49\right\}\)
b: ĐKXĐ: x>1
Để B là số nguyên thì \(3⋮\sqrt{x-1}\)
=>\(\sqrt{x-1}\in\left\{1;3\right\}\)
=>\(x-1\in\left\{1;9\right\}\)
=>\(x\in\left\{2;10\right\}\)
c: ĐKXĐ: x>3
Để C là số nguyên thì \(2⋮\sqrt{x-3}\)
=>\(\sqrt{x-3}\in\left\{1;2\right\}\)
=>\(x-3\in\left\{1;4\right\}\)
=>\(x\in\left\{4;7\right\}\)
giá trị của biểu thức \(\dfrac{1}{3}.\sqrt{\dfrac{9}{25}}-\left(\dfrac{1}{3}+\dfrac{1}{2}\right)^2\)

\(=\dfrac{1}{3}.\dfrac{3}{5}-\left(\dfrac{5}{6}\right)^2\\ =\dfrac{1}{5}-\dfrac{25}{36}\\ =-\dfrac{89}{180}\)

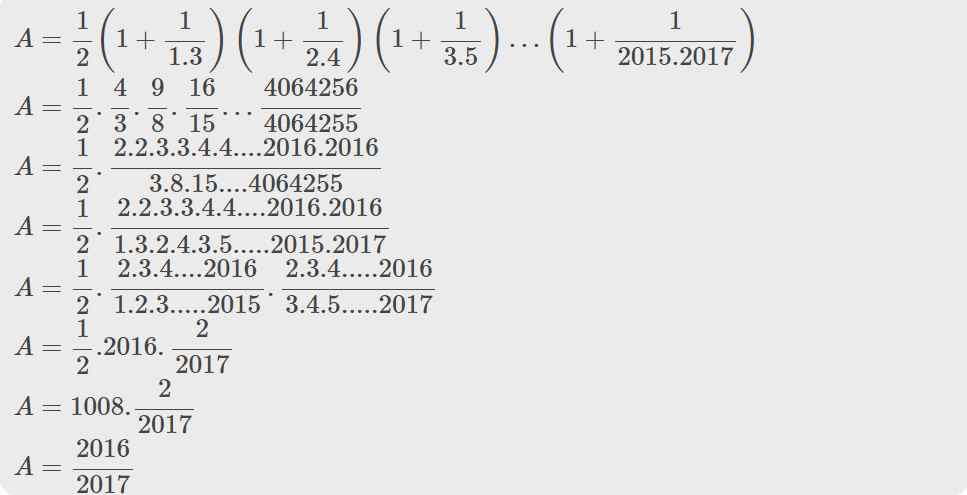
\(A=\dfrac{1}{2}.\left(1+\dfrac{1}{1.3}\right)\left(1+\dfrac{1}{2.4}\right)\left(1+\dfrac{1}{3.5}\right)....\left(\dfrac{1}{2015.2017}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1}.\dfrac{2}{3}\right).\left(\dfrac{3}{2}.\dfrac{3}{4}\right).\left(\dfrac{4}{3}.\dfrac{4}{5}\right)....\left(\dfrac{2016}{2015}.\dfrac{2016}{2017}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{2}{1}.\dfrac{2}{3}\right).\left(\dfrac{3}{2}.\dfrac{3}{4}\right).\left(\dfrac{4}{3}.\dfrac{4}{5}\right).....\left(\dfrac{2016}{2015}.\dfrac{2016}{2017}\right)\)
\(=\dfrac{2016}{2017}\)

\(\dfrac{1-\dfrac{1}{\sqrt{49}}+\dfrac{1}{49}-\dfrac{1}{\left(7\sqrt{7}\right)^2}}{\dfrac{\sqrt{64}}{2}-\dfrac{4}{7}+\left(\dfrac{2}{7}\right)^2-\dfrac{4}{343}}=\dfrac{1-\dfrac{1}{7}+\dfrac{1}{49}-\dfrac{1}{343}}{4-\dfrac{4}{7}+\dfrac{4}{49}-\dfrac{4}{343}}\\ =\dfrac{1-\dfrac{1}{7}+\dfrac{1}{49}-\dfrac{1}{343}}{4\cdot\left(1-\dfrac{1}{7}+\dfrac{1}{49}-\dfrac{1}{343}\right)}=\dfrac{1}{4}\)

\(A=\dfrac{1}{2}\left(\dfrac{2.2}{1.3}\right).\left(\dfrac{3.3}{2.4}\right)...\left(\dfrac{2020.2020}{2019.2021}\right)\)
\(=\dfrac{1.2.2.3.3...2020.2020}{1.2.2.3.3.4.4...2019.2021}\)
\(=\dfrac{1}{2021}\)
\(A=\dfrac{1}{2}\cdot\left(1+\dfrac{1}{1\cdot3}\right)\left(1+\dfrac{1}{2\cdot4}\right)\left(1+\dfrac{1}{3\cdot5}\right)...\left(1+\dfrac{1}{2019\cdot2021}\right)\)
\(A=\dfrac{1}{2}\left(1+\dfrac{1}{2^2-1}\right)\left(1+\dfrac{1}{3^2-1}\right)\left(1+\dfrac{1}{4^2-1}\right)...\left(1+\dfrac{1}{2020^2-1}\right)\)
\(A=\dfrac{1}{2}\cdot\dfrac{2^2}{\left(2-1\right)\left(2+1\right)}\cdot\dfrac{3^2}{\left(3-1\right)\cdot\left(3+1\right)}...\left(\dfrac{2020^2}{\left(2020-1\right)\cdot\left(2020+1\right)}\right)\)
\(A=\dfrac{1}{2}\cdot\dfrac{2}{1}\cdot\dfrac{2}{3}\cdot\dfrac{3}{2}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{2020}{2019}\cdot\dfrac{2020}{2021}\)
\(A=\dfrac{1}{2}\cdot\dfrac{2}{1}\cdot\dfrac{3}{2}\cdot...\cdot\dfrac{2020}{2019}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{2020}{2021}\)
\(A=\dfrac{1}{2}\cdot2020\cdot\dfrac{2}{2021}=\dfrac{2020}{2021}\)

a) \(A=\dfrac{1}{\sqrt{25}}+\dfrac{\sqrt{49}}{\sqrt{36}}-\dfrac{2}{\sqrt{100}}.\)
\(=\dfrac{1}{5}+\dfrac{7}{6}-\dfrac{1}{5}.\)
\(=\left(\dfrac{1}{5}-\dfrac{1}{5}\right)+\dfrac{7}{6}.\)
\(=0+\dfrac{7}{6}=\dfrac{7}{6}.\)
Vậy \(A=\dfrac{7}{6}.\)
b) \(B=\sqrt{\dfrac{0,01}{1,21}}+3.\dfrac{2}{\sqrt{10^2}+2^2+40}-\dfrac{3}{4}.\)
\(=\dfrac{1}{11}+3.\dfrac{2}{10+4+40}-\dfrac{3}{4}.\)
\(=\dfrac{1}{11}+3.\dfrac{1}{37}-\dfrac{3}{4}.\)
\(=\dfrac{1}{11}+\dfrac{1}{9}-\dfrac{3}{4}.\)
\(=\dfrac{36}{396}+\dfrac{44}{396}-\dfrac{297}{296}.\)
\(=-\dfrac{217}{396}.\)
Vậy \(B=-\dfrac{217}{396}.\)
\(S=\dfrac{1}{2}.\left(\dfrac{2}{\sqrt{1.3}}+\dfrac{2}{\sqrt{3.5}}+.......+\dfrac{2}{\sqrt{29.31}}\right)\)
\(S=\dfrac{1}{2}\left(1-\dfrac{1}{\sqrt{3}}+\dfrac{1}{\sqrt{3}}-\dfrac{1}{\sqrt{5}}+\dfrac{1}{\sqrt{5}}+.....-\dfrac{1}{\sqrt{29}}+\dfrac{1}{\sqrt{29}}-\dfrac{1}{\sqrt{31}}\right)\)
\(S=\dfrac{1}{2}.\left(1-\dfrac{1}{\sqrt{31}}\right)=\dfrac{1}{2}.\left(\dfrac{31-\sqrt{31}}{31}\right)=\dfrac{31-\sqrt{31}}{62}\)