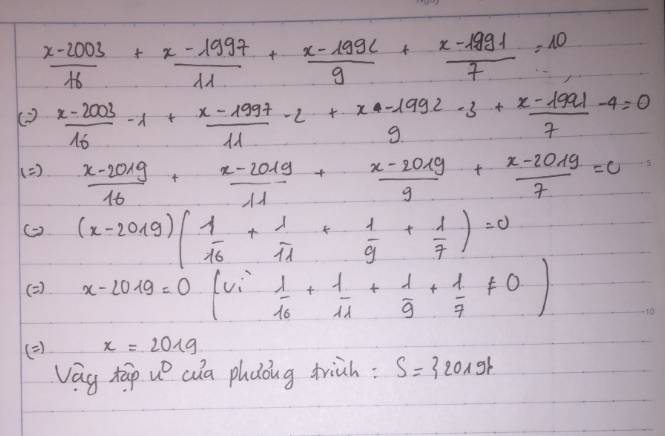`(x-2003)/16 +(x-1997)/11 +(x-1992)/9 +(x-1991)/7=10`

`<=>((x-2003)/16-1)+((x-1997)/11-2)+((x-1992)/9-3)+((x-1991)/7-4)=0`

`<=>(x-2019)/16+ (x-2019)/11 +(x-2019)/9+(x-2019)/7 =0`

`<=> (x-2019)(1/16+1/11+1/9+1/7)=0`

<=> x-2019=0`

`<=> x=2019`

a) 1012 = (100 + 1)2 = 1002 + 2.100 + 1 = 10000 + 200 + 1 = 10201

b) 1992 = (200 – 1)2 = 2002 – 2.200 + 1 = 40000 – 400 + 1 = 39601

c) 47.53 = (50 – 3)(50 + 3) = 502 – 32 = 2500 – 9 = 2491.

a) 39601.              b) 9801.             c) 249001.            d) 89999.

 1992+(-53)+153+(-247)+(-1592)

=[1992+(-1592)]+[(-53)+153]+(-247)

=(-400)+100+(-247)

=(-300)+(-247)

=-547

Ta có: \(\dfrac{1992x}{xy+1992x+1992}\)=

\(\dfrac{xyz.x}{xy+xyz.x+xyz}\) = \(\dfrac{xyz.x.z}{xy.z+xyz.x.z+xyz.z}\) = \(\dfrac{xz}{1+xz+z}\)

Ta có: \(\dfrac{y}{zy+y+1992}\)=\(\dfrac{y}{zy+y+xyz}\)=\(\dfrac{1}{z+1+xz}\)

=> \(\dfrac{1992x}{xy+1992x+1992}\)+\(\dfrac{y}{zy+y+1992}\)+\(\dfrac{z}{z+zx+1}\) = \(\dfrac{xz}{1+zx+z}\) +\(\dfrac{1}{z+zx+1}\) \(+\dfrac{z}{z+zx+1}\) =\(\dfrac{z+zx+1}{z+xz+1}\)

=1

A = x(x – 2009) – y(2009 – x)

ó A = x(x – 2009) + y(x – 2009)

ó A = (x + y)(x – 2009)

Với x =3009 và y = 1991, giá trị của biểu thức là:

A = (3009 + 1991)(3009 – 2009) = 5000.1000 = 5000000

Đáp án cần chọn là:A