A = ((20 + 1) . 20 : 2) . 2 = 420

B = (25 + 20) . 6  : 2 = 135

C = ( 33 + 26) . 8 : 2 = 236

D = (1 + 100) .100 : 2 = 5050

Toán lướp 9 dễ như vậy à bạn

a)  A B   =   A C . sin C   =   8 . sin 54 °   =   6 , 47   ( c m )

b) Trong tam giác ACD, kẻ đường cao AH.

Ta có:  A H   =   A C   .   sin A C H   =   8 . sin 74 °   7 , 69   ( c m )

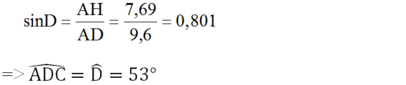
Với mọi số tự nhiên a> 1 ta có:

 \(\frac{1}{\sqrt{a}}=\frac{2}{2\sqrt{a}}>\frac{2}{\sqrt{a}+\sqrt{a+1}}=2\left(\sqrt{a+1}-\sqrt{a}\right)=2\sqrt{a+1}-2\sqrt{a}\)

\(\frac{1}{\sqrt{a}}=\frac{2}{2\sqrt{a}}< \frac{2}{\sqrt{a}+\sqrt{a-1}}=2\left(\sqrt{a}-\sqrt{a-1}\right)=2\sqrt{a}-2\sqrt{a-1}\)

Áp dụng vào bài tập trên ta có:

\(S=1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{144}}\)

\(>2\sqrt{2}-2\sqrt{1}+2\sqrt{3}-2\sqrt{2}+2\sqrt{4}-2\sqrt{3}+...+2\sqrt{145}-2\sqrt{144}\)

\(=-2\sqrt{1}+2\sqrt{145}>2\left(\sqrt{145}-1\right)>2\left(\sqrt{144}-1\right)=22\)

=> S>22

\(S=1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{144}}\)

\(< 1+2\sqrt{2}-2\sqrt{1}+2\sqrt{3}-2\sqrt{2}+...+2\sqrt{144}-2\sqrt{143}\)

\(=1-2\sqrt{1}+2\sqrt{144}=23\)

=> S<23

Vậy 22<S<23

B = 2 + 2 2 − 1 + 2 − 2 2 − 1 = ( 2 − 1 + 1 ) 2 + ( 2 − 1 − 1 ) 2 = 2 − 1 + 1 + 1 − 2 − 1 = 2