Đáp án A

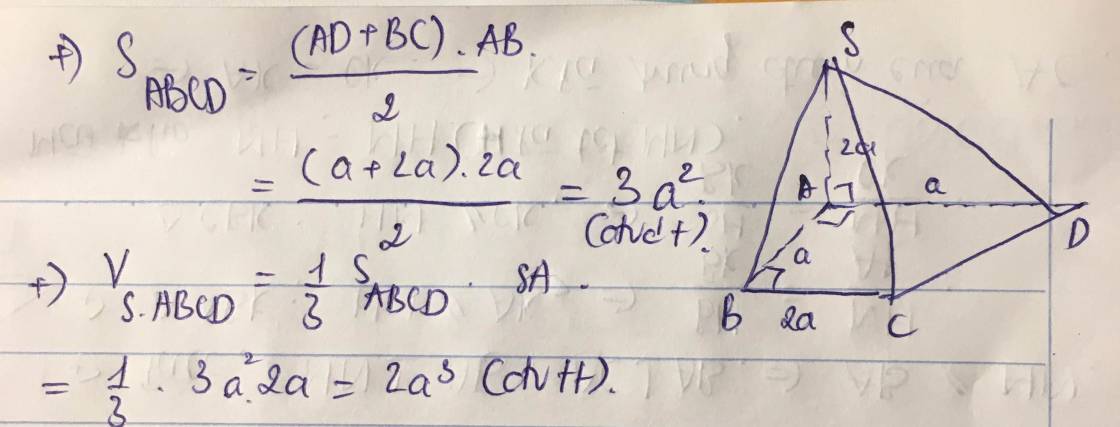
ABCD là hình thanh cân có AB = BC = CD = a; AD = 2a nên M là tâm của đáy ABCD.

SA = AD = 2a; SA ⊥ (ABCD) => tam giác SAD vuông cân tại A nên tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm N của SD

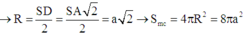
\(V=\dfrac{1}{3}SA.S_{ABCD}=\dfrac{1}{3}SA.\dfrac{1}{2}\left(AD+BC\right).AB=a^3\)

Đáp án C

Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)

Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)

Vậy d(A,(SCD))=AH

Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)

Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)

$E=AB\cap CD,G=EN\cap SB\Rightarrow G$ là trọng tâm tam giác SAE.

$d\left(M,\left(NCD\right)\right)=\frac{GM}{GB}d\left(B,\left(NCD\right)\right)=\frac{1}{2}d\left(B,\left(NCD\right)\right)=\frac{1}{2}.\frac{1}{2}d\left(A,\left(NCD\right)\right)=\frac{1}{4}d\left(A,\left(NCD\right)\right)=\frac{1}{4}h$ 

Tứ diện AEND vuông tại đỉnh A nên $\frac{1}{h^2}=\frac{1}{A{N}^2}+\frac{1}{A{E}^2}+\frac{1}{A{D}^2}=\frac{11}{6a^2}\Rightarrow h=\frac{a\sqrt{66}}{11}$ 

Vậy $d\left(M,\left(NCD\right)\right)=\frac{a\sqrt{66}}{44}.$ 

1: SA vuông góc (ABCD)

=>SA vuông góc AB

=>ΔSAB vuông tại A

SA vuông góc (ABCD)

=>SA vuông góc AD

=>ΔSAD vuông tại A

4: (SD;(ABCD))=(DS;DA)=góc SDA

tan SDA=SA/AD=1/2

=>góc SDA=27 độ

(SC;(ABCD))=(CS;CA)=góc SCA

AC=căn a^2+a^2=a*căn 2

tan SCA=SA/AC=1/căn 2
=>góc SCA=35 độ

Tham khảo

thanks