
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bạn nên viết đề bằng công thức toán để mọi người hiểu đề hơn

\(I=\int\limits^{\sqrt{3}}_0\dfrac{x^2}{1+x^2}dx=\int\limits^{\sqrt{3}}_0\left(1-\dfrac{1}{1+x^2}\right)dx\)
\(=\left(x-arctan\left(x\right)\right)|^{\sqrt{3}}_0=\sqrt{3}-\dfrac{\pi}{3}\)

\(I=\int\limits^{\dfrac{\pi}{4}}_0xsinxdx\)
Đặt \(\left\{{}\begin{matrix}u=x\\dv=sinxdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=-cosx\end{matrix}\right.\)
\(\Rightarrow I=-x.cosx|^{\dfrac{\pi}{4}}_0+\int\limits^{\dfrac{\pi}{4}}_0cosxdx=\left(-x.cosx+sinx\right)|^{\dfrac{\pi}{4}}_0=-\dfrac{\pi\sqrt{2}}{8}+\dfrac{\sqrt{2}}{2}\)

= -2³/3 + 2²/2 + 2.2 - [-(-1)³/3 + (-1)²/2 + 2.(-1)]
= -8/3 + 2 + 4 - 1/3 - 1/2 + 2
= 8 - 3 - 1/2
= 9/2
\(\int\limits^2_{-1}\left(-x^2+x+2\right)dx=\left(-\dfrac{x^3}{3}+\dfrac{x^2}{2}+2x\right)|^2_{-1}=\dfrac{9}{2}\)

\(\int_1^2\sqrt{1+x}dx=\int_1^2\sqrt{1+x}d(1+x)=\dfrac{2}{3}(1+x)^{3/2}|_1^2=...\)

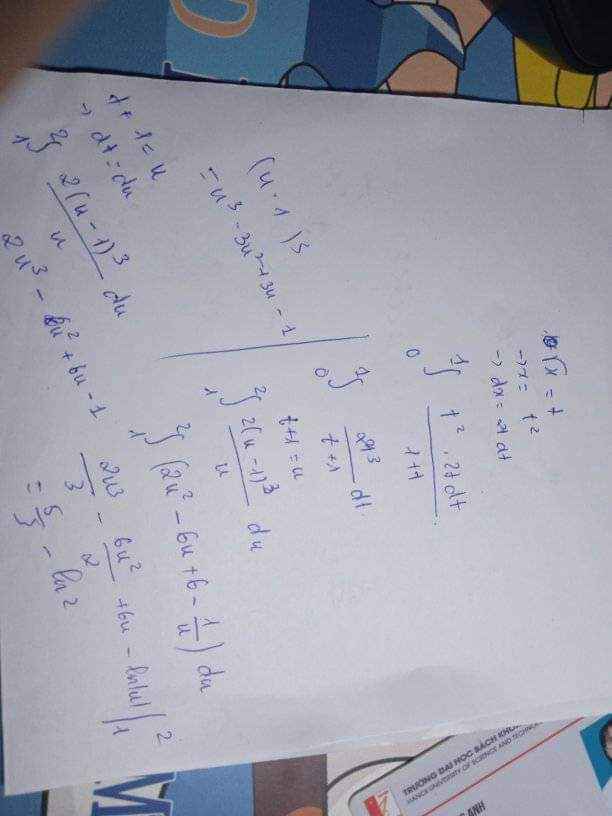
\(I=\int\limits^{100}_0x\left(x-1\right)...\left(x-100\right)dx\)
Đặt \(100-x=t\Rightarrow dx=-dt;\left\{{}\begin{matrix}x=0\Rightarrow t=100\\x=100\Rightarrow t=0\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^0_{100}\left(100-t\right)\left(99-t\right)...\left(1-t\right)\left(-t\right).\left(-dt\right)\)
\(I=\int\limits^0_{100}\left(-1\right)\left(t-100\right).\left(-1\right)\left(t-99\right)...\left(-1\right)\left(t-1\right)\left(-1\right)t\left(-dt\right)\) (101 số -1)
\(I=-\int\limits^0_{100}t\left(t-1\right)\left(t-2\right)...\left(t-100\right)\left(-dt\right)\)
\(I=-\int\limits^{100}_0t\left(t-1\right)\left(t-2\right)...\left(t-100\right)dt\)
\(I=-\int\limits^{100}_0x\left(x-1\right)\left(x-2\right)...\left(x-100\right)dx=-I\)
\(\Rightarrow2I=0\Rightarrow I=0\)