Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(100+98+96+...+2-97-95-93-...-3\)
= \(100+98+\left(96-97\right)+\left(94-95\right)+...+\left(2-3\right)\)
= \(100+98-95\) = \(103\)
b) \(2-4-6+8+10-12-14+16+...-102+104\)
= \(\left(2-4\right)+\left(-6+8\right)+\left(10-12\right)+\left(-14+16\right)+...+\left(-102+104\right)\)
= \(-2+2-2+2-2+...+2\) = \(0\)
c) \(1+2-3-4+5+6-7-8+9+10-11-12+...-111-112+113+114\)
= \(\left(1+2\right)-\left(3+4\right)+\left(5+6\right)-\left(7+8\right)+...\left(113+114\right)\)
= \(3-7+11-15+19-23+...+219-223+227\)
= \(\left(3-7\right)+\left(11-15\right)+\left(19-23\right)+...+\left(219-223\right)+227\)
= \(-4-4-4-4-...-4+227\)
= \(54\left(-4\right)+227\) = \(-216+227\) = \(11\)

nhưng mình hỏi 2 lần một lần là 11 một lần là 115 cho nên mình hơi phân vân! xin lỗi nhé!

8.
\(\Leftrightarrow sin^4x-cos^2x=2sinx.cosx\)
Nhận thấy \(cosx=0\) không phải nghiệm, chia 2 vế cho \(cos^4x\) ta được:
\(tan^4x-\dfrac{1}{cos^2x}=2tanx.\dfrac{1}{cos^2x}\)
\(\Leftrightarrow tan^4x-\left(1+tan^2x\right)=2tanx\left(1+tan^2x\right)\)
\(\Leftrightarrow tan^4x-2tan^3x-tan^2x-2tanx-1=0\)
Wel well, đề bài sai, phương trình bậc 4 này không giải được

Lời giải:
Số số lập được: \(A^4_9=3024\)
Tính tổng:
Trong số 3024 số được lập ra, mỗi chữ số $1,2,3,...,9$ xuất hiện $8.7.6=336$ lần ở mỗi vị trí hàng nghìn- trăm- chục - đơn vị.
Do đó tổng các số tìm được là:
$(1+2+3+...+9).336(10^3+10^2+10+1)=16798320$

Chọn C
Ta có ![]()
Gọi số tự nhiên cần tìm có bốn chữ số là a b c d ¯
Vì a b c d ¯ chia hết cho 11 nên (a + c) - (b + d) ⋮ 11
=> (a + c) - (b + d) = 0 hoặc (a + c) - (b + d) = 11 hoặc (a + c) - (b + d) = -11 do
![]()
![]()
Theo đề bài ta cũng có a + b + c + d chia hết cho 11
Mà ![]()
![]()
![]()
![]() hoặc
hoặc ![]()
Vì ![]()
![]() nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ
nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ

![]()
(do các trường hợp còn lại không thỏa mãn) => (a,c) và (b,d) là một trong các cặp số:
![]()
- Chọn 2 cặp trong số 4 cặp trên ta có C 4 2 cách.
- Ứng với mỗi cách trên có 4 cách chọn a; 1 cách chọn c; 2 cách chọn b; 1 cách chọn d.
![]()
Vậy xác suất cần tìm là 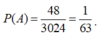

Các bộ 3 số thỏa mãn: (1;2;7);(1;3;6);(1;4;5);(2;3;5) tổng cộng 4 bộ số
Với mỗi bộ số ta có \(3!\) cách hoán vị
Do đó có: \(3!.4=24\) số

Ta thấy:
a) Số sau hơn số liền trước 3 đơn vị.
b) Số sau hơn số liền trước 2 đơn vị.
c) Số sau hơn số liền trước 5 đơn vị.
d) Số sau hơn số liền trước 3 đơn vị.
Điểm giống nhau của các dãy số này là hai số hạng liền nhau hơn kém nhau một số không đổi.

Bài 2:
a: \(=\dfrac{7}{9}\left(\dfrac{7}{6}-\dfrac{19}{20}-\dfrac{1}{15}\right)+\dfrac{22}{5}\cdot\dfrac{1}{24}\)
\(=\dfrac{7}{9}\cdot\dfrac{3}{20}+\dfrac{22}{120}=\dfrac{7}{60}+\dfrac{11}{60}=\dfrac{18}{60}=\dfrac{3}{10}\)
b: \(=\left(\dfrac{35-32}{60}\right)^2+\dfrac{4}{5}\cdot\dfrac{70-45}{80}\)
\(=\dfrac{1}{400}+\dfrac{4\cdot25}{400}=\dfrac{101}{400}\)
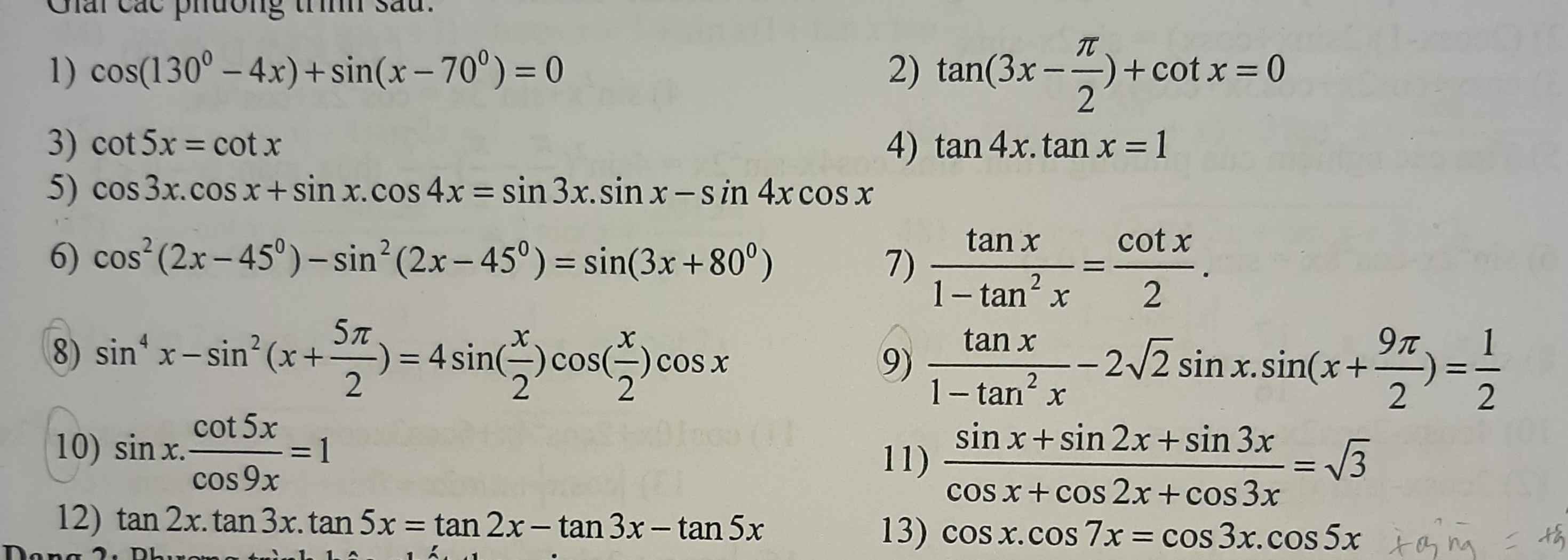
Hờ, bài toán này mà mình cứ ngồi tính tổng như thật -,-
\(\text{1 + 2 - 3 - 4 + 5 + 6 - 7 - 8 + 9 + 10 - 11 - 12 + ... - 111 - 112 + 113 + 114}\)\(=1+\left(2-3-4+5\right)+\left(6-7-8+9\right)+\left(10-11-12+13\right)+...+\left(110-111-112+113\right)+114\)\(=1+114=115\)
Lớp 5: chương trình nâng cao nhé các bạn! ko có số âm nhé!