Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Đặt t = 2x + 2-x, suy ra t2 = 22x + 2 -2x + 2.
Ta có ![]()
Phương trình trở thành
![]()
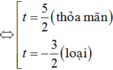
![]()
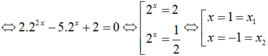
khi đó ; S = x1+ x2 = 0.

Đặt \(t=2^x\)
Phương trình sẽ trở thành:
\(-t^2+3t-2=0\)
=>\(\left(t^2-3t+2\right)=0\)
=>\(\left(t-1\right)\left(t-2\right)=0\)
=>\(\left[{}\begin{matrix}t=1\\t=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2^x=1\\2^x=2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
\(x_1+x_2=0+1=1\)

a) \(2^{x+4}+2^{x+2}=5^{x+1}+3\cdot5^x\)
\(\Rightarrow2^x+2^4+2x^x+2^2=5^x\cdot x+3\cdot5^x\)
\(\Leftrightarrow2^x+16+2^x\cdot4=5\cdot5^x+3\cdot5^x\)
\(\Leftrightarrow16\cdot2^x+4\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot\left(\dfrac{2}{5}\right)^x=8\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\dfrac{2}{5}\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\left(\dfrac{2}{5}\right)^1\)
\(\Rightarrow x=1\)

ĐKXĐ: \(x>-1\)
Bước quan trọng nhất là tách hàm
\(\Leftrightarrow log_2\sqrt{x+3}-2\sqrt{x+3}+\left(x+3\right)=log_2\left(x+1\right)-2\left(x+1\right)+\left(x+1\right)^2\)
Đến đây coi như xong \(\Rightarrow\sqrt{x+3}=x+1\Rightarrow x=1\)

Đáp án B.
Với x ∈ 5 2 ; 4 thì phương trình tương đương với:
m - 1 log 2 2 x - 2 + m - 5 log 2 x - 2 + m - 1 = 0 (1)
Đặt log 2 ( x - 2 ) = t . Với x ∈ 5 2 ; 4 thì t ∈ - 1 ; 1 . Phương trình (1) trở thành:
( m - 1 ) t 2 + ( m - 5 ) t + m - 1 = 0 ⇔ m ( t 2 + t + 1 ) = t 2 + 5 t + 1 ⇔ m = t 2 + 5 t + 1 t 2 + t + 1 (2)
Xét hàm số f ( t ) = t 2 + 5 t + 1 t 2 + t + 1 = 1 + 4 t t 2 + t + 1 trên đoạn - 1 ; 1 .
Đạo hàm f ' ( t ) = - 4 ( t 2 - 1 ) t 2 + t + 1 ≥ 0 , ∀ t ∈ - 1 ; 1 ; f ' ( t ) = 0 ⇔ t = ± 1 . Khi đó hàm số f ( t ) đồng biến trên - 1 ; 1 . Suy ra min - 1 ; 1 f ( t ) = f ( - 1 ) = - 3 ; max - 1 ; 1 f ( t ) = f ( 1 ) = 7 3 .
Phương trình (2) có nghiệm ⇔ Đường thẳng y - m cắt đồ thị hàm số f ( t ) ⇔ - 3 ≤ m ≤ 7 3 . Vậy S = - 3 ; 7 3 → a = - 3 , b = 7 3 → a + b = - 3 + 7 3 = - 2 3 .
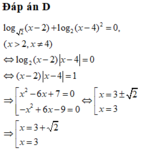


Chọn A