ĐẤM NHAU

Căn cứ vào đề 

\(\widehat{O2}=150^0;\widehat{O4}=150^0\)

\(\Rightarrow\widehat{O2}=\widehat{O4}\)

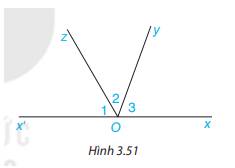
a) Ta có: \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = (\widehat {{O_1}} + \widehat {{O_2}}) + \widehat {{O_3}}\)=\(\widehat {x'Oy} + \widehat {{O_3}}\), mà \(\widehat {x'Oy} + \widehat {{O_3}}\)= 180\(^\circ \) ( 2 góc kề bù)

Vậy \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ \)

b) Vì \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ \)

\(\begin{array}{l} \Rightarrow 60^\circ  + \widehat {{O_2}} + 70^\circ  = 180^\circ \\ \Rightarrow \widehat {{O_2}} = 180^\circ  - 60^\circ  - 70^\circ  = 50^\circ \end{array}\)

Vậy \(\widehat {{O_2}} = 50^\circ \)

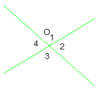
Cho hình vẽ. Tính  O 1 ^ , O 2 ^ , O 3 ^ , O 4 ^  nếu biết:

a) Vì O 1 ^ + O 2 ^ = 180 0  ( Hai góc kề bù)  mà O 1 ^ = 1 2 O 2 ^ nên

1 2 O 2 ^ + O 2 ^ = 180 0 ⇒ 3 2 O 2 ^ = 180 0 ⇒ O 2 ^ = 180 0 .2 3 = 120 0

O 1 ^ = 1 2 O 2 ^ ⇒ O 1 ^ = 1 2 .120 0 = 60 0

Vậy  O 1 ^ = O 3 ^ = 60 0 ; O 2 ^ = O 4 ^ = 120 0

b) Vì  O 1 ^ + O 2 ^ = 180 0 ( Hai góc kề bù)  mà  O 2 ^ − O 1 ^ = 40 0

⇒ 2 O 2 ^ = 220 0 ⇒ O 2 ^ = 110 0

O 2 ^ − O 1 ^ = 40 0 ⇒ 120 0 − O 1 ^ = 40 0 ⇒ O 1 ^ = 70 0

Vậy  O 1 ^ = O 3 ^ = 70 0 ; O 2 ^ = O 4 ^ = 110 0

c) O 1 ^ + O 3 ^ = 130 0  Mà O 1 ^ = O 3 ^ ( Đối đỉnh) nên  O 1 ^ = O 3 ^ = 130 0 : 2 = 65 0

O 2 ^ = O 4 ^ = 180 0 − 65 0 = 115 0 ( Hai góc kè bù)

d)  O 1 ^ + O 2 ^ + O 3 ^ = 250 0

Vì O 1 ^ + O 2 ^ = 180 0 ( Hai góc kề bù) nên O 3 ^ = 250 0 − 180 0 = 70 0 .

Do đó O 1 ^ = O 3 ^ = 70 0 ( Đối đỉnh)

O 2 ^ = 180 0 − 70 0 = 110 0 . Suy ra O 4 ^ = O 2 ^ = 110 0 ( Đối đỉnh)

e)  O 1 ^ + O 3 ^ = 1 2 ( O 2 ^ + O 4 ^ )

Mà  O 1 ^ = O 3 ^ ( Đối đỉnh) , O 4 ^ = O 2 ^ ( Đối đỉnh)

Suy ra  2 O 1 ^ = 1 2 .2 O 2 ^ ⇒ 2 O 1 ^ = O 2 ^

Vì O 1 ^ + O 2 ^ = 180 0 ( Hai góc kề bù). Suy ra  O 1 ^ + 2 O 1 ^ = 180 0 ⇒ O 1 ^ = 60 0

O 1 ^ = O 3 ^ = 60 0 ; O 2 ^ = 2 O 1 ^ = 60 0 .2 = 120 0   ⇒ O 4 ^ = O 2 ^ = 120 0

\(1,\widehat{A}+\widehat{B}+\widehat{C}=180^0\\ \text{Mà }\widehat{A}=\widehat{B}=\widehat{C}\\ \Rightarrow\widehat{A}=\widehat{B}=\widehat{C}=\dfrac{180^0}{3}=60^0\\ 2,\widehat{A}+\widehat{B}+\widehat{C}=180^0\\ \Rightarrow\widehat{B}+\widehat{C}=180^0-\widehat{A}=110^0\\ \text{Mà }\widehat{B}-\widehat{C}=10^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{B}=\left(110^0+10^0\right):2=60^0\\\widehat{C}=60^0-10^0=50^0\end{matrix}\right.\)

O1=O3=85⁰; O2=O4=95⁰

Ta có O1 + O2 =180 độ(kề bù)

Mà O2-O1=10 độ

Suy ra O2=95 độ;O1=85 độ

Suy ra O2=O4=95 độ(đđ);O1=O3=85 độ

Giải:

Ta có:

\(\widehat{O_2}+\widehat{O_1}=180^o\) ( kề bù ) và \(\widehat{O_2}-\widehat{O}_1=10^o\)

\(\Rightarrow\widehat{O_1}=\left(180^o-10^o\right):2=85^o\)

\(\Rightarrow\widehat{O}_2=85^o+10^o=95^o\)

\(\Rightarrow\widehat{O_1}=\widehat{O_3}=85^o\) ( đối đỉnh )

\(\Rightarrow\widehat{O}_2=\widehat{O_4}=95^o\) ( đối đỉnh )

Vậy \(\widehat{O_1}=85^o;\widehat{O_2}=95^o;\widehat{O_3}=85^o;\widehat{O_4}=95^o\)

cảm ơn bạn nhiều

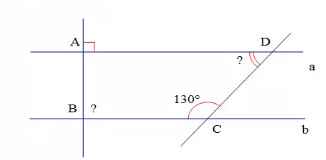
\(a//b;a\perp AB\Rightarrow b\perp AB\Rightarrow\widehat{B}=90^0\)

\(a//b\Rightarrow\widehat{D}+\widehat{C}=180^0\left(trong.cùng.phía\right)\\ \Rightarrow\widehat{D}=180^0-130^0=50^0\)

a,Ta thấy \(\widehat{B}\) là góc vuông

\(\Rightarrow\widehat{B}=90^o\)

\(\widehat{C}+\widehat{D}=180^o\)(bù nhau)

\(\Rightarrow\widehat{D}=180^o-130^o=50^o\)