K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LN
2 tháng 12 2021
Giải:
Hình thang CDHG có: CE = GE , DF = HF ( gt )
=> EF là đường TB của hình thang.
=> EF = \(\dfrac{CD+GH}{2}\) = \(\dfrac{12+16}{2}\) = 14 cm ( hay y = 14 cm )
Hình thang ABFE có: AC = CE, BD = DF ( gt )
=> CD là đường TB của hình thang trên.
=> CD = \(\dfrac{AB+EF}{2}\)
mà CD = 12 cm, EF = 14 cm ( cmt )
=> AB = 12.2 - 14 = 10 cm ( hay x = 10 cm )
Vậy x = 10 cm, y = 14 cm
PT
1
CM
9 tháng 7 2017
+ Tính x :
AB // EF nên tứ giác ABFE là hình thang
Hình thang ABFE có: CA = CE và DB = DF
⇒ CD là đường trung bình của hình thang ABFE
⇒ CD = (AB + EF)/2
hay x = (8 + 16)/2 = 12(cm)
+ Tính y:
CD // GH nên tứ giác CDHG là hình thang
Hình thang CDHG có : EC = EG, FD = FH
⇒ EF là đường trung bình của hình thang CDHG
⇒ EF = (CD + GH)/2
hay (x + y)/2 = 16cm ⇒ x + y = 32cm
Mà x = 12cm ⇒ y = 20cm.
Vậy x = 12cm và y = 20cm.
22 tháng 11 2017
AB // EF nên ABFE là hình thang CA = CE và DB = DF nên CD là đường trung bình của hình thang ABFE
Do đó : \(CD=\frac{AB+EF}{2}=\frac{8+16}{2}=12\)
hay x = 12
Tương tự CDHG là hình thang , EF là đường trung bình hình thang CDHG
Do đó : \(EF=\frac{CD+GH}{2}\Rightarrow GH=2EF-CD=2.16-12=20\)
hay y = 20
Vaayj x = 12 ; y = 20
HV
1
2 tháng 1 2023
\(\dfrac{AB}{CD}=\dfrac{EF}{GH}\)
=>\(\dfrac{AB}{CD}+1=\dfrac{EF}{GH}+1\)
=>\(\dfrac{AB+CD}{CD}=\dfrac{EF+GH}{GH}\)
AB/CD=EF/GH
nên CD/AB=GH/EF
=>\(\dfrac{CD}{AB}+1=\dfrac{GH}{EF}+1\)
=>\(\dfrac{CD+AB}{AB}=\dfrac{GH+EF}{EF}\)
=>\(\dfrac{AB}{CD+AB}=\dfrac{EF}{EF+GH}\)
NB
0
SG
1
H
21 tháng 4 2017
Bài giải:
AB // EF nên ABFE là hình thang CA = CE và DB = DF nên CD là đường trung bình của hình thang ABFE.
Do đó: CD = \(\dfrac{AB+EF}{2}\) = \(\dfrac{8+16}{2}\) = 12
Hay x = 12
Tương tự CDHG là hình thang, EF là đường trung bình của hình thang CDHG.
Nên EF = \(\dfrac{CD+GH}{2}\) => GH = 2EF -CD = 2.16 - 12
GH = 20 hay y = 20
Vậy x = 12, y = 20
CM
8 tháng 1 2019
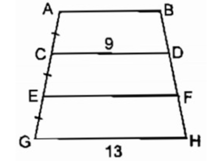
Chọn đáp án C. 7 và 11
Ta có : hình thang CDHG có : CD//GH và CE = EG
=> F là trung điểm của DH
=> EF là đường trung bình của hình thang CDHG => EF = (CD + HG)/2 = (9 + 13)/2 = 11
Ta có : hình thang ABFE có: AB//EF và AC = CE
=> D là trung điểm của BF
Suy ra: CD là đường trung bình của hình thang ABFE
=> CD = (AB + EF)/2 => AB= 2CD - EF => AB = 2.9 - 11 = 7
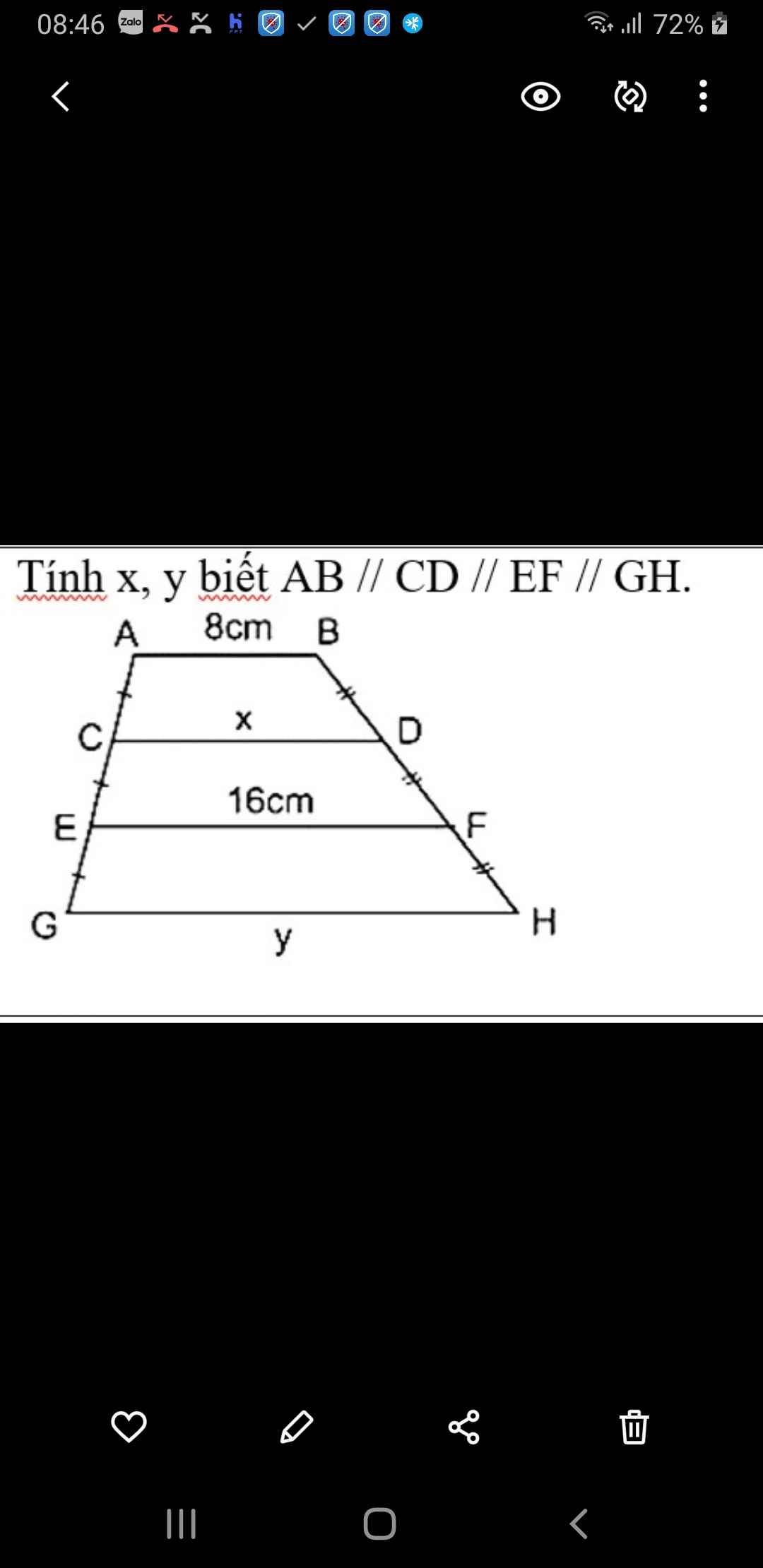
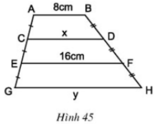
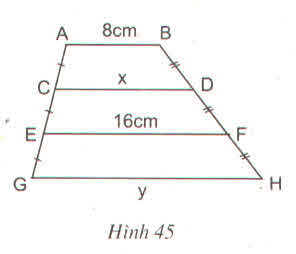
\(AB//EF\) nên \(ABFE\) là hình thang
\(\left\{{}\begin{matrix}AC=CE\\BD=BF\end{matrix}\right.\Rightarrow CD\) là đường trung bình hình thang \(ABFE\)
\(\Rightarrow x=CD=\dfrac{AB+EF}{2}=\dfrac{24}{2}=12\left(cm\right)\)
\(CD//GH\) nên \(CDHG\) là hình thang
\(\left\{{}\begin{matrix}CE=EG\\HF=FD\end{matrix}\right.\Rightarrow EF\) là đường trung bình hình thang \(CDHG\)
\(\Rightarrow EF=16=\dfrac{CD+GH}{2}=\dfrac{12+y}{2}\\ \Rightarrow12+y=32\Rightarrow y=20\left(cm\right)\)