
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(({x^2} + 2x + 3) + (3{x^2} - 5x + 1) = ({x^2} + 3{x^2}) + (2x - 5x) + (3 + 1) = 4{x^2} - 3x + 4\);
b) \(\begin{array}{l}(4{x^3} - 2{x^2} - 6) - ({x^3} - 7{x^2} + x - 5) = 4{x^3} - 2{x^2} - 6 - {x^3} + 7{x^2} - x + 5\\ = (4{x^3} - {x^3}) + ( - 2{x^2} + 7{x^2}) - x + ( - 6 + 5) = 3{x^3} + 5{x^2} - x - 1\end{array}\);
c) \(\begin{array}{l} - 3{x^2}(6{x^2} - 8x + 1) = - 3{x^2}.6{x^2} - - 3{x^2}.8x + - 3{x^2}.1\\ = - 18{x^{2 + 2}} + 24{x^{2 + 1}} - 3{x^2} = - 18{x^4} + 24{x^3} - 3{x^2}\end{array}\);
d) \(\begin{array}{l}(4{x^2} + 2x + 1)(2x - 1) = (4{x^2} + 2x + 1).2x - (4{x^2} + 2x + 1).1 = 4{x^2}.2x + 2x.2x + 1.2x - 4{x^2} - 2x - 1\\ = 8{x^{2 + 1}} + 4{x^{1 + 1}} + 2x - 4{x^2} - 2x - 1 = 8{x^3} + 4{x^2} + 2x - 4{x^2} - 2x - 1 = 8{x^3} - 1\end{array}\);
e) \(\begin{array}{l}({x^6} - 2{x^4} + {x^2}):( - 2{x^2}) = {x^6}:( - 2{x^2}) - 2{x^4}:( - 2{x^2}) + {x^2}:( - 2{x^2})\\ = - \dfrac{1}{2}{x^{6 - 2}} + {x^{4 - 2}} - \dfrac{1}{2}{x^{2 - 2}} = - \dfrac{1}{2}{x^4} + {x^2} - \dfrac{1}{2}.\end{array}\);
g)

\(({x^5} - {x^4} - 2{x^3}):({x^2} + x)=x^3-2x^2\)

Dễ
Thế
Mà
Cũnhoir
Dc
Ạ
Chịu
Chắc
Phải
Ngu
Lamqs
Mới
Hỏi
Câu
Này

a)
\(\dfrac{1}{2}{x^2}.\dfrac{6}{5}{x^3} = \dfrac{1}{2}.\dfrac{6}{5}.{x^2}.{x^3} = \dfrac{3}{5}{x^5}\);
b)
\(\begin{array}{l}{y^2}(\dfrac{5}{7}{y^3} - 2{y^2} + 0,25) = {y^2}.\dfrac{5}{7}{y^3} - {y^2}.2{y^2} + {y^2}.0,25)\\ = \dfrac{5}{7}{y^5} - 2{y^4} + 0,25{y^2}\end{array}\);
c)
\(\begin{array}{l}(2{x^2} + x + 4)({x^2} - x - 1) \\= 2{x^2}({x^2} - x - 1) + x({x^2} - x - 1) + 4({x^2} - x - 1)\\ = 2{x^4} - 2{x^3} - 2{x^2} + {x^3} - {x^2} - x + 4{x^2} - 4x - 4 \\= 2{x^4} - {x^3} + {x^2} - 5x - 4\end{array}\);
d)
\(\begin{array}{l}(3x - 4)(2x + 1) - (x - 2)(6x + 3) \\= 3x(2x + 1) - 4(2x + 1) - x(6x + 3) + 2(6x + 3)\\ = 6{x^2} + 3x - 8x - 4 - 6{x^2} - 3x + 12x + 6\\ = 4x + 2\end{array}\).

a)
\(\begin{array}{l}R(x) + S(x) = - 8{x^4} + 6{x^3} + 2{x^2} - 5x + 1 + {x^4} - 8{x^3} + 2x + 3\\ = ( - 8 + 1){x^4} + (6 - 8){x^3} + 2{x^2} + ( - 5 + 2)x + (1 + 3)\\ = - 7{x^4} - 2{x^3} + 2x - 3x + 4\end{array}\)
b)
\(\begin{array}{l}R(x) - S(x) = - 8{x^4} + 6{x^3} + 2{x^2} - 5x + 1 - ({x^4} - 8{x^3} + 2x + 3)\\ = - 8{x^4} + 6{x^3} + 2{x^2} - 5x + 1 - {x^4} + 8{x^3} - 2x - 3\\ = ( - 8 - 1){x^4} + (6 + 8){x^3} + 2{x^2} + ( - 5 - 2)x + (1 - 3)\\ = - 9{x^4} + 14{x^3} + 2x - 7x - 2\end{array}\)

a) \(\begin{array}{l}(8{x^3} + 2{x^2} - 6x):(4x) = 8{x^3}:(4x) + 2{x^2}:(4x) - (6x):(4x)\\ = (8:4).({x^3}:x) + (2:4).({x^2}:x) - (6:4).(x:x)\\ = 2{x^2} + \dfrac{1}{2}x - \dfrac{3}{2}\end{array}\)
b) \(\begin{array}{l}(5{x^3} - 4x):( - 2x) = 5{x^3}:( - 2x) - 4x:( - 2x) = (5: - 2).({x^3}:x) - (4: - 2).(x:x)\\ = - \dfrac{5}{2}{x^{3 - 1}} - ( - 2) = - \dfrac{5}{2}{x^2} + 2\end{array}\)
c) \(\begin{array}{l}( - 15{x^6} - 24{x^3}):( - 3{x^2}) = ( - 15{x^6}):( - 3{x^2}) + ( - 24{x^3}):( - 3{x^2})\\ = ( - 15: - 3).({x^6}:{x^2}) + ( - 24: - 3).({x^3}:{x^2})\\ = 5.{x^{6 - 2}} + 8.{x^{3 - 2}} = 5{x^4} + 8x\end{array}\)

a: =1/2x^3*x^2-1/2x^3*6x-1/2x^3*10
=1/2x^5-3x^4-5x^3
b: =-3x^2*5x^3+3x^2*4x^2-3x^2*3x+3x^2*3x
=-15x^5+12x^4-9x^3+9x^2
c: \(=3x\cdot5x^2-3x\cdot2x-3x=15x^3-6x^2-3x\)
d: \(=\dfrac{1}{2}x^2y\cdot2x^3-\dfrac{1}{2}x^2y\cdot\dfrac{2}{5}xy^2-\dfrac{1}{2}x^2y=x^5y-\dfrac{1}{5}x^3y^3-\dfrac{1}{2}x^2y\)

a) \( - 2{x^2} + 6{x^2} = ( - 2 + 6).{x^2} = 4{x^2}\);
b) \(4{x^3} - 8{x^3} = (4 - 8).{x^3} = - 4{x^3}\);
c) \(3{x^4}( - 6{x^2}) = 3.( - 6).{x^4}.{x^2} = - 18{x^{4 + 2}} = - 18{x^6}\);
d) \(( - 24{x^6}):( - 4{x^3}) = ( - 24: - 4).({x^6}:{x^3}) = 6{x^{6 - 3}} = 6{x^3}\).
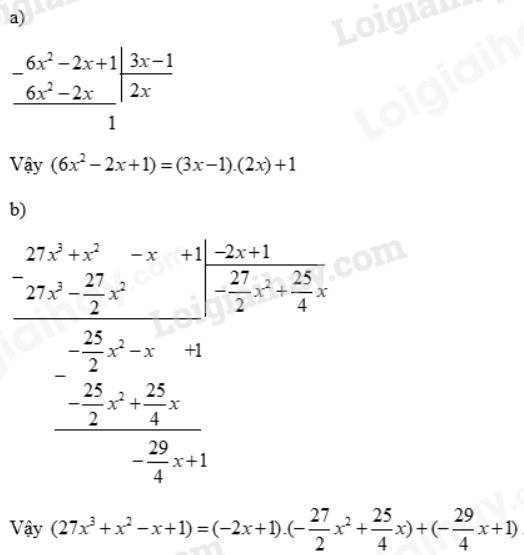


a)
Vậy \(({x^3} + 1):({x^2} - x + 1) = x + 1\).
b)
Vậy \((8{x^3} - 6{x^2} + 5) = ({x^2} - x + 1)(8x + 2) + ( - 6x + 3)\)