
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = \(\dfrac{3^{123}+1}{3^{125}+1}\) Vì 3123 + 1 < 2125 + 1 Nên A = \(\dfrac{3^{123}+1}{3^{125}+1}\)< \(\dfrac{3^{123}+1+2}{3^{125}+1+2}\)
A < \(\dfrac{3^{123}+3}{3^{125}+3}\) = \(\dfrac{3.\left(3^{122}+1\right)}{3.\left(3^{124}+1\right)}\) = \(\dfrac{3^{122}+1}{3^{124}+1}\) = B
Vậy A < B

Tính nhanh
a) 72. (-50).(-2).(-2)
b) 125.(-5).(-20).8
c) 125.(-3).(-32).(-4)
d) (-123 – 123-123-123).125


\(-23-24-25+123+124+125\\ =\left(123-23\right)+\left(124-24\right)+\left(125-25\right)\\ =100+100+100\\ =300\)

Số số hạng của dẫy số là: (126- 24) :1+ 1=103 (số hạng)
Tổng dẫy số là: \(\frac{\left(126+24\right).103}{2}=7725\)
Số số hạng của dãy só đó là : ( 126 - 24 ) : 1 + 1 = 103 ( số )
Tổng của dãy số đó là : ( 126 + 24 ) x 103 : 2 = 7725
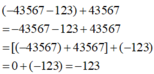
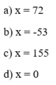
Đáp án là A
Ta có: (-43567 - 123) + 43567 = -43567 - 123 + 43567
= [(-43567) + 43567] + (-123) = 0 + (-123) = -123