n kxdvjslkdx;q['ă

gọi số thứ 1 là x ĐK x,y >0

--------------2----y

do tỉ số giữa 2 số là 3/5 => 5x=3y  (1)

số thứ 1 chia 9 bé hơn số thứ 2 chia 6 là 3 đơn vị nên ta có phương trình

y/6 - x/9 = 3  (2)

từ (1) và (2) ta có hệ phương trình 

........

x=18  y=30

vậy ........

cau ntn

Gọi a (a ∈ N *) là số thứ nhất. Ta có số thứ hai là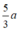 

Thương phép chia số thứ nhất cho 9 là a/9

Thương phép chia số thứ hai cho 6 là: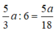 

Thương thứ nhất bé hơn thương thứ hai là ba đơn vị nên ta có phương trình:

5a/18 - a/9 = 3

⇔ 5a/18 - 2a/18 = 54/18

⇔ 5a – 2a = 54

⇔ 3a = 54 ⇔ a = 18 (thỏa mãn)

Vậy số thứ nhất là 18, số thứ hai là 5/3.18 = 30.

Lời giải:
Gọi hai số phải tìm là $a,b$. Theo bài ra ta có:

$a+b=94$

$\frac{a}{4}-\frac{b}{9}=4$

Thay $a=94-b$ ta được:

$\frac{94-b}{4}-\frac{b}{9}=4$

$\Leftrightarrow 23,5-(\frac{b}{4}+\frac{b}{9})=4$

$\Leftrightarrow 23,5-\frac{13}{36}b=4$
$\Leftrightarrow \frac{13}{36}b=19,5$

$\Leftrightarrow b=54$

$a=94-b=94-54=40$ 

Gọi x là mẫu số, 4/5x là tử số (x,y thuộc N*)
Theo đề bài:Nếu lấy số thứ nhất chia cho 4 , số thứ hai chia cho 3 thì thương thứ nhất bé hơn thương thứ hai 2 đơn vị nên:

\(\frac{x}{3}-\frac{\frac{4}{5}x}{4}=2\)
=> x= 15
vậy số cần tìm là 12 và 15

Gọi 2 số cần tìm lần lượt là a, b \(\left(a,b\inℕ^∗\right)\)

Tỉ số giữa số thứ nhất và số thứ 2 là \(\frac{4}{7}\)\(\Rightarrow\frac{a}{b}=\frac{4}{7}\)\(\Rightarrow\frac{a}{4}=\frac{b}{7}\)

Đặt \(\frac{a}{4}=\frac{b}{7}=k\left(k\inℕ^∗\right)\)\(\Rightarrow a=4k\)và \(b=7k\)

Nếu lấy số thứ nhất chia cho 4, số thứ 2 chia cho 5 thì thương số thứ nhất bé hơn thương thứ hai 2 đơn vị

\(\Rightarrow\)Ta có phương trình: \(\frac{7k}{5}-\frac{4k}{4}=2\)

\(\Leftrightarrow\frac{28k}{20}-\frac{20k}{20}=\frac{40}{20}\)\(\Leftrightarrow8k=40\)\(\Leftrightarrow k=5\)( thoả mãn điều kiện )

\(\Rightarrow a=4.5=20\); \(b=5.7=35\)

Vậy số bé là 20 và số lớn là 35

+) Gọi số thứ nhất (ban đầu) là x. (x: nguyên, dương)

Khi đó số thứ hai (ban đầu) là \(\dfrac{3}{5}x\)

+) Số thứ nhất sau khi chia cho 9 gọi là \(\dfrac{x}{9}\)

Số thứ hai sau khi chia cho 6 gọi là \(\dfrac{\dfrac{3}{5}x}{6}\)

Vì: thương số thứ nhất chia cho 9 bé hơn thương số thứ hai chia cho 6 là 3 đơn vị nên ta có phương trình:

\(\dfrac{x}{9}+3=\dfrac{\dfrac{3}{5}x}{6}\\ < =>\dfrac{2x}{18}+\dfrac{54}{18}=\dfrac{\dfrac{9}{5}x}{18}\\ < =>2x+54=\dfrac{9}{5}x\\ < =>2x-\dfrac{9}{5}x=-54\\< =>\dfrac{1}{5}x=-54\\ =>x=\dfrac{-54}{\dfrac{1}{5}}=-270\left(loại\right)\)

Vậy: Không thỏa mãn yêu cầu đề bài.