Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Tổng số trận đấu trong giải đấu là: ![]()
Sau mỗi trận hòa, tổng số điểm 2 đội nhận được là 1.2 =2.
Sau mỗi trận không hòa, tổng số điểm 2 đội nhận được là 3 + 0 = 3.
Tổng số điểm của tất cả các đội sau khi kết thúc giải đấu là:
65.2 + (182 – 65).3 = 481.

1.
Gọi số đó là \(\overline{abcd}\)
- Nếu d=0 \(\Rightarrow abc\) có \(A_7^3=210\) cách chọn và hoán vị
- Với \(d\ne0\Rightarrow d\) có 4 cách chọn, bộ \(abc\) có \(A_7^3-A_6^2=180\) cách \(\Rightarrow180.4=720\) cách
Vậy có \(210+720=930\) số thỏa mãn
2.
Số cách thỏa mãn: \(A_{11}^5=55440\)
3.
Số cách lấy 3 bi không quan tâm xanh đỏ: \(C_8^1.C_{10}^2=360\)
Số cách lấy toàn bi đỏ: \(C_5^1C_6^2=75\)
Số cách lấy toàn bi xanh: \(C_3^1C_4^2=18\)
Số cách thỏa mãn: \(360-\left(75+18\right)=...\)

Đáp án A
Số cách lấy ra 4 ứng viên bất kỳ từ 16 ứng viên là ![]() cách.
cách.
- Gọi A là biến cố “4 ứng viên lấy được có đúng một ứng viên 10 tuổi và không quá hai ứng viên 12 tuổi”. Ta xét ba khả năng sau:
- Số cách lấy 1 10 tuổi, 3 11 tuổi là: ![]()
- Số cách lấy 1 10 tuổi, 2 11 tuổi, 1 12 tuổi là: ![]()
- Số cách lấy 1 10 tuổi, 1 11 tuổi, 2 12 tuổi là: ![]()
Xác suất của biến cố A là 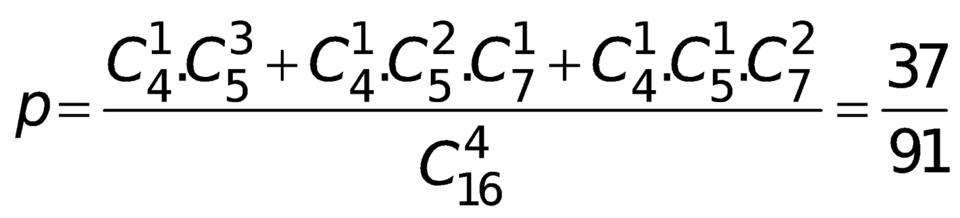 .
.

Những trận đấu giữa Real Madrid và Barcelona luôn rất rất căng thẳng và đỉnh điểm chính là trong giai đoạn 1953-1966 và 2010-2013

Đáp án B
Gọi A là biến cố “Cú sút đó không vào lưới”. Nếu cầu thủ sút vào vị trí 1 hoặc 2, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 = 1 8 . Nếu cầu thủ sút cào vị trí 3 hoặc 4, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 . 1 2 = 1 16 . Suy ra xác suất để bóng không vào bằng P ( A ) = 1 8 + 1 16 = 3 16 .

Số trận đấu sao cho hai đội bất kì trong 16 đội tham gia gặp nhau đúng một lần là:
C 16 2 = 120 trận

Số vận động viên được khảo sát là \(n = 3 + 8 + 12 + 12 + 4 = 39\).
Gọi \({x_1};{x_2};...;{x_{39}}\) là thời gian luyện tập của 39 vận động viên được xếp theo thứ tự không giảm. Ta phải chọn các vận động viên có thời gian luyện tập tương ứng là \({x_{30}};{x_{31}};...;{x_{39}}\)
Ta có:
\({x_1},{x_2},{x_3} \in \left[ {0;2} \right);{x_4},...,{x_{11}} \in \left[ {2;4} \right);{x_{12}},...,{x_{23}} \in \left[ {4;6} \right);{x_{24}},...,{x_{35}} \in \left[ {6;8} \right);{x_{36}},...,{x_{39}} \in \left[ {8;10} \right)\). Vậy \({x_{30}}\) thuộc nhóm \(\begin{array}{*{20}{l}}{\left[ {6;8} \right)}\end{array}\).
Ta có: \(n = 29;{n_j} = 12;C = 3 + 8 + 12 = 23;{u_j} = 6;{u_{j + 1}} = 8\)
\({x_{30}} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 6 + \frac{{\frac{{3.39}}{4} - 23}}{{12}}.\left( {8 - 6} \right) \approx 7,04\)
Vậy huấn luyện viên nên chọn các vận động viên có thời gian luyện tập từ 7,04 giờ trở lên.


ta có \(A^5_{11}=55440\)
Có 55440 cách chọn ra 5 cầu thủ trong 11 cầu thủ của đội