Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì M thuộc đường trung trực của đoạn thẳng AB nên MA = MB.
Vì N thuộc đường trung trực của đoạn thẳng AB nên NA = NB.
+) Xét ∆AMN và ∆BMN có:
MA = MB ( chứng minh trên)
NA = NB (chứng minh trên)
MN chung
Suy ra: ∆AMN = ∆BMN (c.c.c) nên các khẳng định (A), (B), (C) sai, (D) đúng.

a) Ta có: đường thẳng a là đường trung trực của đoạn thẳng AB và CD nên \(a \bot AB;a \bot CD\).
Suy ra: AB // CD.
b) Đường thẳng a là đường trung trực của đoạn thẳng AB và CD nên MN là đường trung trực của đoạn thẳng AB và CD. Suy ra: MD = MC.
Xét tam giác vuông MNC và tam giác vuông MND có: ND = NC; MD = MC.
Vậy \(\Delta MNC = \Delta MND\)(cạnh huyền – cạnh góc vuông).
c) \(\Delta MNC = \Delta MND\)nên \(\widehat {CMN} = \widehat {DMN}\).
Mà \(\widehat {AMN} = \widehat {BMN} = 90^\circ \Rightarrow \widehat {AMN} - \widehat {DMN} = \widehat {BMN} - \widehat {CMN}\).
Vậy \(\widehat {AMD} = \widehat {BMC}\).
d) Xét hai tam giác AMD và BMC có:
MA = MB;
\(\widehat {AMD} = \widehat {BMC}\);
MD = MC.
Vậy \(\Delta MAD = \Delta MBC\)(c.g.c). Suy ra: \(AD = BC,\widehat A = \widehat B\) (cặp cạnh và góc tương ứng).
e) \(\Delta MAD = \Delta MBC\) nên \(\widehat {ADM} = \widehat {BCM}\) (2 góc tương ứng).
\(\Delta MNC = \Delta MND\) nên \(\widehat {MCN} = \widehat {MDN}\) (2 góc tương ứng).
Vậy \(\widehat {ADM} + \widehat {MDN} = \widehat {BCM} + \widehat {MCN}\) hay \(\widehat {ADC} = \widehat {BCD}\).

a: Xét ΔOMA và ΔOMB có
OM chung
MA=MB
OA=OB
Do đó: ΔOMA=ΔOMB
Xét ΔONA và ΔONB có
ON chung
NA=NB
OA=OB
Do đó: ΔONA=ΔONB
b: Ta có: OA=OB
nen O nằm tren đường trung trực của AB(1)
Ta có: MA=MB
nen M nằm trên đường trung trực của AB(2)
Ta có: NA=NB
nên N nằm trên đường trung trực của AB(3)
TỪ (1), (2)và (3) suy ra O,M,N thẳng hàng
c: Xét ΔAMN và ΔBMN có
AM=BM
MN chung
AN=BN
Do đó ΔAMN=ΔBMN

Xét tg AMN và tg BMN có:
MN chung
MA = MB (gt)
NA = NB (gt)
=> tg AMN = tg BMN (c.c.c)
1) Giả thiết: \(\Delta AMN;\Delta BMN\) có: MA = MB và NA = NB.
Kết luận: tg AMN = tg BMN
2) \(\Delta AMN\) và \(\Delta BMN\) có:
MN: cạnh chung
MA = MB (giả thiết)
NA = NB (giả thiết)
Do đó \(\Delta AMN=\Delta BMN\left(c.c.c\right)\)
Suy ra \(\widehat{AMN}=\widehat{BMN}\) (2 góc t/ư).
bạn làm sai chỗ Kết luận: tg AMN = tg BMN VÌ ngta nói chứng minh góc chứ ko phải tg

a) Xét \(\Delta\)OMA và \(\Delta\)OMB:
OA = OB (đề bài)
AM = BM (vì có cùng bán kính)
Cạnh OM chung
=> \(\Delta\)OMA = \(\Delta\)OMB (c.c.c)
Xét \(\Delta\)ONA và \(\Delta\)ONB
OA = OB (đề bài)
AN = BN (vì cò cùng bán kính)
Cạnh ON chung
=> \(\Delta\)ONA = \(\Delta\)ONB (c.c.c)
b) Ta có \(\Delta\)OMA = \(\Delta\)OMB (theo câu a)
=> ^AOM = ^BOM (2 góc tương ứng)
=> OM là tia phân giác của ^AOB
Lại có \(\Delta\)ONA = \(\Delta\)ONB (theo câu a)
=> ^AOM = ^BOM (2 góc tương ứng)
=> ON là tia phân giác của ^AOB
Mà mỗi góc chỉ có duy nhất một tia phân giác
=> OM và ON trùng nhau
hay O, M, N thẳng hàng (ĐPCM)
c) Xét \(\Delta\)AMN và \(\Delta\)BMN
AM = BM (vì có cùng bán kính)
AN = BN (vì có cùng bán kính)
cạnh MN chung
=> \(\Delta\)AMN = \(\Delta\)BMN (c.c.c)
d) Ta có \(\Delta\)AMN = \(\Delta\)BMN (theo câu c)
=> ^AMN = ^BMN (2 góc tương ứng)
=> MN là tia phân giác của ^AMB

Vì D nằm giữa A và C nên tia BD nằm giữa 2 tia BA và BC
\(\Rightarrow\widehat{ABC}=\widehat{ABD}+\widehat{DBC}\)
\(\Rightarrow\widehat{DBC}=\widehat{ABC}-\widehat{ABD}=25^o\)

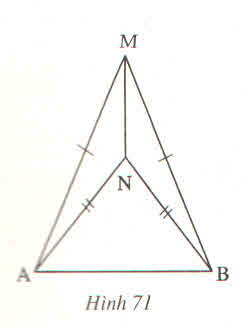
Chọn D