Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

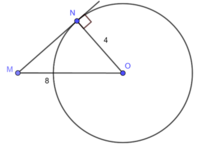
Vì MN là tiếp tuyến của đường tròn (O) tại N nên
Xét tam giác vuông MNO có:
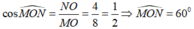
Đáp án: D

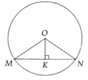
a, Tính được OK = R 2
b, Tính được
M
O
K
^
=
60
0
;
M
O
N
^
=
120
0
c, HS tự làm

\(\Delta ADB\text{ cân tại A}\Rightarrow\widehat{ADB}=\dfrac{180^0-\widehat{BAD}}{2}=65^0\\ \text{Ta có }\widehat{MBH}=\widehat{BCD}=\widehat{ADN}=\widehat{BAD}=50^0\\ \Rightarrow\widehat{ODN}=\widehat{ADB}+\widehat{ADN}=115^0\\ MH\text{//}AN\Rightarrow\widehat{MHA}=\widehat{HAN}\\ \Rightarrow\widehat{MHB}+\widehat{MBH}=\widehat{BAD}+\widehat{NAD}\\ \Rightarrow\widehat{MHB}=\widehat{NAD}\\ \Rightarrow\Delta MHB\sim\Delta AND\left(g.g\right)\\ \Rightarrow\dfrac{MB}{AD}=\dfrac{HB}{ND}\Rightarrow MB\cdot NC=AD\cdot HB\left(1\right)\)
\(\left\{{}\begin{matrix}\widehat{OHB}=\widehat{AOD}=90^0\\\widehat{HBO}=\widehat{ODA}\end{matrix}\right.\Rightarrow\Delta HBO\sim\Delta ODA\\ \Rightarrow\dfrac{HB}{OD}=\dfrac{OB}{AD}\Rightarrow HB\cdot AD=OB\cdot OD\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow\dfrac{MB}{OD}=\dfrac{OB}{ND}\\ \text{Mà }\widehat{MBO}=\widehat{NDO}\\ \Rightarrow\Delta MBO\sim\Delta ODN\left(c.g.c\right)\\ \Rightarrow\widehat{MOB}=\widehat{OND}\Rightarrow\widehat{MOB}+\widehat{NOD}=\widehat{OND}+\widehat{NOD}\\ \Rightarrow\widehat{MOB}+\widehat{NOD}=180^0-\widehat{NDO}=65^0\\ \Rightarrow180^0-\widehat{MON}=65^0\\ \Rightarrow\widehat{MON}=115^0\)
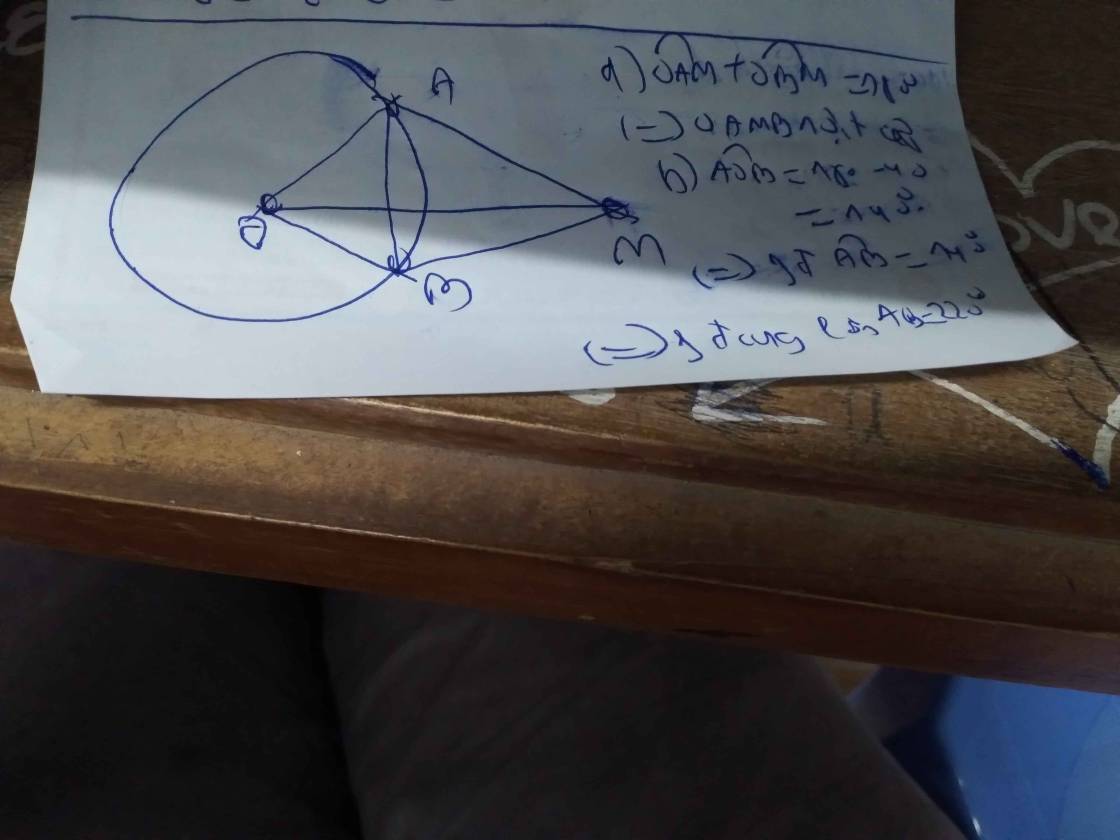
Ta có:
Mà
Đáp án: (B)