Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
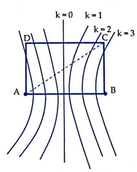
Từ hình vẽ ta thấy để trên CD có 5 điểm dao động với biên độ cực đại thì điểm C phải nằm giữa đường cực đại bậc 2 và đường cực đại bậc 3
⇒ 2 λ ≤ A C − B C < 3 λ ⇔ 2 λ ≤ A B 2 + B C 2 − B C < 3 λ ⇔ 2 λ ≤ A B 2 + 3 4 A B 2 − 3 4 A B < 3 λ ⇔ 2 λ ≤ A B 2 + 3 4 A B 2 − 3 4 A B < 3 λ ⇔ 2 λ ≤ A B 2 < 3 λ ⇔ 4 ≤ A B λ < 6
Vậy A B λ (phần nguyên của A B λ ) giá trị lớn nhất là 5
Suy ra, số cực đại tối đa trên AB là 2 A B λ + 1 = 11 đ i ể m

Đáp án B
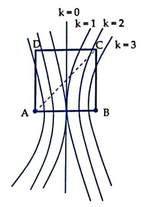
Từ hình vẽ ta thấy để CD có 3 điểm dao động với biên độ cực đại thì điểm C phải nằm giữa đường cực đại bậc 2 và đường cực đại bậc 3
⇒ 2 λ ≤ C A − C B < 3 λ ⇔ 2 λ ≤ A B 2 − A B ≤ 3 λ ⇔ 2 λ ≤ A B 2 − 1 < 3 λ
⇔ 2 2 − 1 ≤ A B λ < 3 2 − 1 ⇔ 4 , 8 ≤ A B λ < 7 , 24
Gọi A B λ là phần nguyên của tỉ số A B λ
Số điểm dao động với biên độ cực đại trên AB là N = 2 A B λ + 1
Mà N m a x khi A B λ max = 7
Suy ra, số điểm cực đại trên AB nhiều nhất là 2.7+1=15 điểm

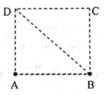
+ Xét hình vuông ABCD có cạnh bằng a.
+ Số cực đại trên CD thỏa điều kiện:
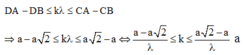
+ Vì trên CD có 3 cực đại và các cực đại đối xứng qua cực đại
![]()
+ Số cực đại trên AB:
![]()
=> Chọn D.

Đáp án D
Số cực đại trên CD thõa mãn điều kiện :

Vì trên CD có 3 cực đại và các cực đại đối xứng qua cực đại k = 0 nên : -2 < k < 2

Số cực đại trên AB
![]()
Số cực đại là 9.
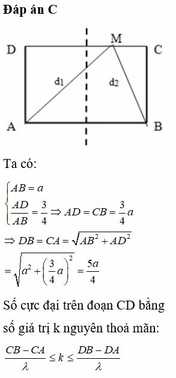




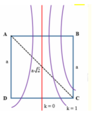
Đáp án C
Từ hình vẽ ta thấy để trên CD có 5 điểm dao động với biên độ cực đại thì điểm C phải nằm giữa đường cực đại bậc 2 và đường cực đại bậc 3.
Vậy A B λ (phần nguyên của A B λ ) nhận giá trị lớn nhất là 5.
Suy ra, số cực đại tối đa trên AB là 2 A B λ +1=11 điểm.