- Xét phương trình hoành độ giao điểm : \(x^2=2mx-2m+3\)

\(\Leftrightarrow x^2-2mx+2m-3=0\left(I\right)\)

- Xét thấy để P và d cắt nhau tại hai điểm phân biệt khi PT ( I ) có hai nghiệm phân biệt .

\(\Leftrightarrow\Delta^,=b^{,2}-ac=m^2-\left(2m-3\right)>0\)

\(\Leftrightarrow m^2-2m+3>0\)

Mà \(m^2-2m+3=m^2-2m+1+2=\left(m+1\right)^2+2\ge2>0\forall m\in R\)

Vậy ... ĐPCM

a, Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình:

\(x^2=2mx+1\)

\(\Leftrightarrow x^2-2mx-1=0\)

Ta có: \(\Delta'=\left(-m\right)^2-1.\left(-1\right)=m^2+1\)

Vì \(m^2\ge0\forall m\Rightarrow\) \(m^2+1\ge1>0\forall m\) \(\Leftrightarrow\Delta'>0\forall m\)

Vậy với mọi m thì đường thẳng (d) và parabol (P) cắt nhau tại 2 điểm phân biệt.

Phương trình hoành độ giao điểm:

\(-\dfrac{1}{2}x^2=mx+m-3\Leftrightarrow x^2+2mx+2m-6=0\) (1)

a. Khi \(m=-1\), (1) trở thành:

\(x^2-2x-8=0\Rightarrow\left[{}\begin{matrix}x=4\Rightarrow y=-8\\x=-2\Rightarrow y=-2\end{matrix}\right.\)

Vậy (d) cắt (P) tại 2 điểm có tọa độ là \(\left(4;-8\right)\) ; \(\left(-2;-2\right)\)

b. 

\(\Delta'=m^2-2m+6=\left(m+1\right)^2+5>0;\forall m\Rightarrow\left(1\right)\) có 2 nghiệm pb với mọi m

Hay (d) cắt (P) tại 2 điểm pb với mọi m

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=2m-6\end{matrix}\right.\)

\(x_1^2+x_2^2=14\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=14\)

\(\Leftrightarrow4m^2-2\left(2m-6\right)=14\)

\(\Leftrightarrow4m^2-4m-2=0\Rightarrow m=\dfrac{1\pm\sqrt{3}}{2}\)

b) Phương trình hoành độ giao điểm của (P) và (d) là:

\(x^2=2\left(m-1\right)x+5-2m\)

\(\Leftrightarrow x^2-2\left(m-1\right)x-5+2m=0\)

Áp dụng hệ thức Vi-et, ta được:

\(x_1+x_2=2\left(m-1\right)\)

Ta có: \(x_1+x_2=6\)

\(\Leftrightarrow2\left(m-1\right)=6\)

\(\Leftrightarrow m-1=3\)

hay m=4

Vậy: m=4

b) Phương trình hoành độ giao điểm của (P) và (d) là:

- x 2  = 2mx - 5 ⇔  x 2  + 2mx - 5 = 0

Δ'= m 2 + 5 > 0 với ∀m ∈ R

Vậy trên mặt phẳng Oxy đường thẳng (d) và Parabol (P) luôn cắt nhau tại hai điểm phân biệt.

Khi m = 2, phương trình hoành độ giao điểm của (P) và (d) là:

- x 2 = 4x - 5 ⇔ x 2  + 4x - 5 = 0

Δ = 4 2  - 4.1.(-5) = 36

⇒ Phương trình có 2 nghiệm

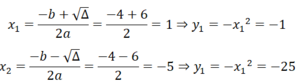
Vậy tọa độ hai giao điểm là M(1;-1) và N(-5;-25)

Phương trình hoành độ giao điểm của (P) và (d) : \(\frac{1}{4}.x^2=mx+1\)  (1)

<=> x² = 4mx + 4 <=> x² - 4mx - 4 = 0

\(\Delta\)' = (-2m)² + 4 = 4m² + 4 \(\ge\) 4 > 0 với mọi m

=> (1) luôn có 2 nghiệm phân biệt 

Vậy (P) luôn cắt (d) tại 2 điểm  phân biệt

b) Gọi 2 nghiệm đó là x₁; x₂

Theo hệ thức Vi ét có: 

 x₁ +  x₂ = 4m

 x₁ x₂ = - 4 < 0

=>  x₁; x₂  trái dấu . 

A; B là 2 giao điểm => A (x₁; mx₁ + 1); B(x₂; mx₂ + 1) . Giả sử x₁ < 0 < x₂

+)  A; B nằm về hai phía của trục tung do  x₁; x₂  trái dấu . 

Gọi H; K lần lượt là hình chiếu của A; B xuống Ox => H(x₁; 0); K(x₂; 0)

Khi đó S _OAB = S _AHKB - S_AHO - S_BKO

S _AHKB = (AH + BK). HK : 2 = (mx₁ + 1 +mx₂ + 1 ) .(- x₁ + x₂) : 2 = \(\frac{\left(m\left(x_1+x_2\right)+2\right)\left(x_2-x_1\right)}{2}=\frac{m\left(x_2^2-x_1^2\right)+2.\left(x_2-x_1\right)}{2}\)

S_AHO = AH.HO : 2 = (mx₁ + 1). (-x₁₎ : 2  = \(\frac{-mx^2_1-x_1}{2}\)

S_BKO = BK.KO : 2 = (mx₂ + 1). x₂ : 2 = \(\frac{mx^2_2+x_2}{2}\)

Vậy S_OAB = \(\frac{m\left(x_2^2-x_1^2\right)+2.\left(x_2-x_1\right)}{2}\)- \(\frac{-mx^2_1-x_1}{2}\) - \(\frac{mx^2_2+x_2}{2}\)

= \(\frac{m\left(x_2^2-x_1^2\right)+2.\left(x_2-x_1\right)+m\left(x_1^2-x_2^2\right)+x_1-x_2}{2}=\frac{x_2-x_1}{2}\)

ta có: \(\left(x_2-x_1\right)^2=x_2^2-2x_2x_1+x_1^2=\left(x_1+x_2\right)^2-4x_1.x_2\)

= (4m)² - 4.(-4) = 16m² + 16

=> x₂ - x₁ = \(\sqrt{16m^2+16}=4.\sqrt{m^2+1}\)

Vậy S_OAB = \(4.\sqrt{m^2+1}\)

 CÁI ĐỀ NÀY 
AI GIÚP TÔI ĐƯỢC KHÔNG CHIỀU MAI TỚ PHẢI NỘP ÙI PLEASE~~~~~!!

BÀI 3:Xác định tham số m để hàm số y=(m^2 - 4)x-5 nghịch biến
Xác định tham số m để hàm số y=(m^2 - 1)x+2 đồng biến với mọi x>0
BÀI 6 Cho đường thẳng (d) y=-x+2 và parabol P y=1/2.x^2 
a)tìm giá trị m để điểm M(m;m-1) nằm trên (d).Với m vừa tìm được chứng tỏ điểm M không thuộc P
b) vẽ P và (d) trên cùng mặt phẳng tọa độ và tìm tọa độ giao điểm của
chúng 
BÀI 4:
TRONG mặt phẳng tọa độ Oxy , cho parabol P: y=-x^2
a) vẽ đồ thị P
b) gọi A và B là hai điểm thuộc P có hoành độ lần lượt là 1 , -2 .Lập phuơng trình đường thẳng AB 
c) tìm phương trình đường thẳng (d) song song với đường thẳng AB và tiếp xúc với P