Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Trong khoảng thời gian từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng giác là bao nhiêu độ?

Đổi 2 giờ 15 phút = \(\frac{9}{4}\)giờ.
Trong khoảng thời gian từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng giác là \(\frac{9}{4}.( - {360^ \circ }) = - {810^ \circ }\)

Ta có: \({u_1} = 1,\;\;{u_2} = 2, \ldots ,{u_{12}} = 12\).
\({u_2} - {u_1} = {u_3} - {u_2} =...={u_{12}} - {u_{11}} = 1\), do đó \(\left( {{u_n}} \right)\) là cấp số cộng với \({u_1} = 1,\;d = 1\).
Tổng số tiếng chuông trong khoảng từ 0 đến 12 giờ trưa là:
\({S_{12}} = \frac{{12 \times \left( {1 + 12} \right)}}{2} = 78\).

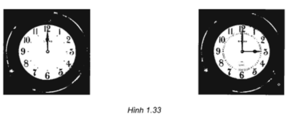
a) Khi kim phút quay theo ngược chiều kim đồng hồ để nó chỉ đúng số 12, kim phút quay:
\(\frac{2}{{12}} = \frac{1}{6}\) phần của vòng tròn
b) Khi kim phút quay theo đúng chiều kim đồng hồ để nó chỉ đúng số 12, kim phút quay:
\(\frac{{10}}{{12}} = \frac{5}{6}\) phần của vòng tròn
c) Có 2 cách quay kim phút theo một chiều xác định để kim phút từ vị trí chỉ đúng số 2 về vị trí chỉ đúng số 12, đó là: ngược chiều kim đồng hồ và cùng chiều kim đồng hồ

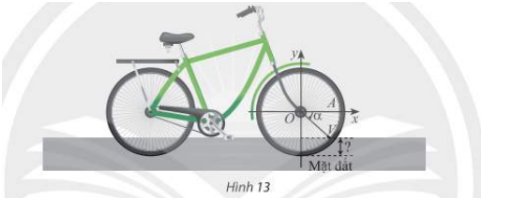
Sau một phút di chuyển, van V đã quay được một góc lượng giác có số đo góc là: \(\alpha=11\cdot60=660\left(rad\right)\)
Khi đó tọa độ điểm V biểu diễn cho góc lượng giác trên có tọa độ là: \(V\left(58\cdot cos\alpha,58\cdot sin\alpha\right)\approx\left(56;15,2\right)\)
Từ đó, khoảng cách từ van đến mặt đất khoảng \(58-15,2\approx42,8\left(cm\right)\)

Lúc 1 giờ đồng hồ đánh 1 tiếng chuông.
Lúc 2 giờ đồng hồ đánh 2 tiếng chuông
......
Lúc 12 giờ trưa đồng hồ đánh 12 tiếng chuông.
Do đó, từ 0 giờ đến 12 giờ trưa, đồng hồ đánh số tiếng chuông là:
1+ 2+ 3+ .... + 11+ 12
Đây là tổng 12 số hạng của cấp số cộng có số hạng đầu u1= 1, công sai d = 1
Vậy tổng số tiếng chuông đồng hồ trong khoảng thời gian từ 0 đến 12 giờ trưa là:
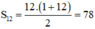



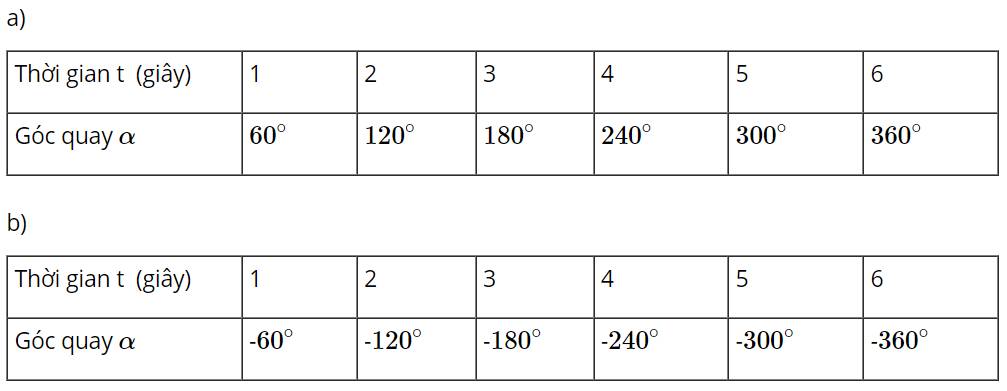
Từ lúc 12 giờ đến 15 giờ kim giờ quay được 1 góc 90o
Từ lúc 12 giờ đến 15 giờ kim phút quay được 1 góc: 3 vòng. 360o=1080o