Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a)
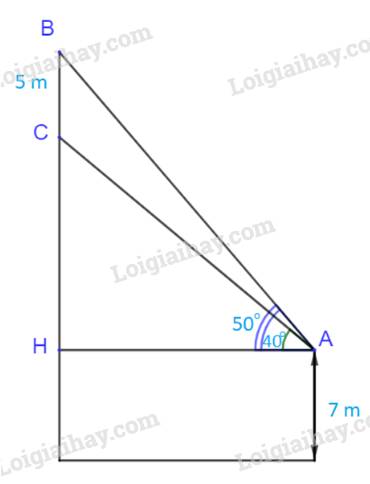
Gọi H là hình chiếu của A lên đường thẳng BC.
Ta có: \(\widehat {HAB} = {50^o}\); \(\widehat {HAC} = {40^o}\)
\( \Rightarrow \widehat {BAC} = {50^o} - {40^o} = {10^o}\) (1)
Xét tam giác ABH, vuông tại H ta có:
\(\widehat H = {90^o};\;\widehat {BAH} = {50^o}.\)
\( \Rightarrow \widehat {HBA} = {180^o} - {90^o} - {50^o} = {40^o}\) hay \(\widehat {CBA} = {40^o}\). (2)
Từ (1) và (2), suy ra: \(\widehat {BCA} = {180^o} - {40^o} - {10^o} = {130^o}.\)
Vậy ba góc của tam giác ABC lần lượt là: \(\widehat A = {10^o};\;\widehat B = {40^o};\;\widehat C = {130^o}\).
b)
Áp dụng định lý sin cho tam giác ABC, ta được:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\) \( \Rightarrow AB = \frac{{BC.\sin C}}{{\sin A}}\)
Mà: \(BC = 5\;(m);\;\;\widehat C = {130^o};\;\widehat A = {10^o}\)
\( \Rightarrow AB = \frac{{5.\sin {{130}^o}}}{{\sin {{10}^o}}} \approx 22\;(m)\)
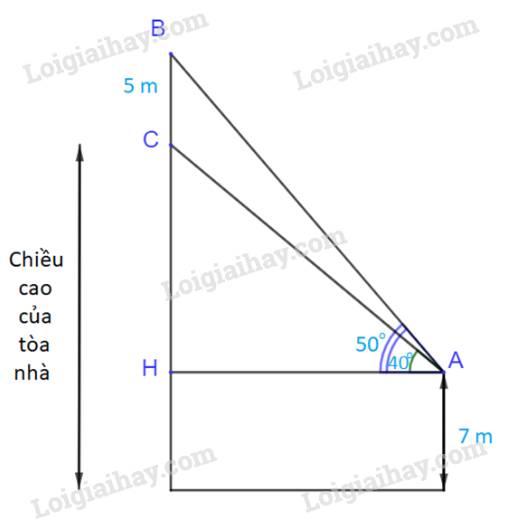
Xét tam giác ABH, vuông tại H ta có:
\(\sin \widehat {BAH} = \frac{{BH}}{{AB}}\)\( \Rightarrow BH = AB.\,\,\sin \widehat {BAH}\)
Mà: \(AB \approx 22\;(m);\;\;\widehat {BAH} = {50^o}\)
\( \Rightarrow BH \approx 22.\sin {50^o} \approx 16,85\;(m)\)
Vậy chiều cao của tòa nhà là: \(BH-{\rm{ }}BC + 7 = 16,85-5 + 7 = 18,85{\rm{ }}\left( m \right)\)

Gọi A là vị trí đứng của Nam, B là điểm cao nhất của cây, C là vị trí gốc cây.
Gọi H là hình chiếu của A trên BC. Ta có hình vẽ:
TH1: Cây cao hơn tòa nhà

Ta có: \(\tan {24^ \circ } = \frac{{BH}}{{AH}} \Rightarrow BH = 30.\tan {24^ \circ } \approx 13,357\)
\( \Rightarrow BC = BH + HC \approx 13,357 + 1,5 + 18,5 = 33,357(m)\)
TH2: Cây thấp hơn tòa nhà
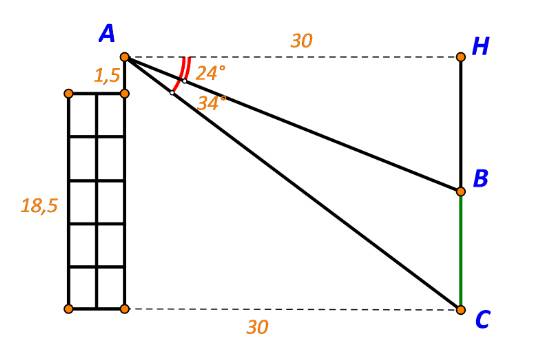
Ta có: \(\tan {24^ \circ } = \frac{{BH}}{{AH}} \Rightarrow BH = 30.\tan {24^ \circ } \approx 13,357\)
\( \Rightarrow BC = HC -HB \approx 1,5 + 18,5 - 13,357= 6,643(m)\)

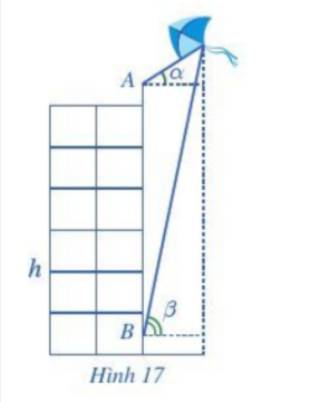
Gọi các điểm:
O là vị trí của chiếc diều.
H là hình chiếu vuông góc của chiếc diều trên mặt đất.
C, D lần lượt là hình chiếu vuông góc của A, B trên OH.
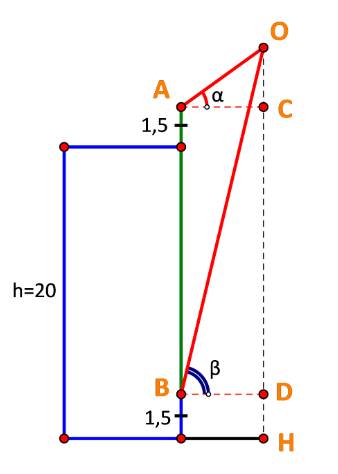
Đặt OC = x, suy ra OH = x + 20 + 1,5 =x + 21,5.
Xét tam giác OAC, ta có: \(\tan \alpha = \frac{{OC}}{{AC}} \Rightarrow AC = \frac{{OC}}{{\tan \alpha }} = \frac{x}{{\tan {{35}^o}}}\)
Xét tam giác OBD, ta có: \(\tan \beta = \frac{{OD}}{{BD}} \Rightarrow BD = \frac{{OD}}{{\tan \beta }} = \frac{{x + 20}}{{\tan {{75}^o}}}\)
Mà:\(AC = BD\)\( \Rightarrow \frac{x}{{\tan {{35}^o}}} = \frac{{x + 20}}{{\tan {{75}^o}}}\)
\(\begin{array}{l} \Leftrightarrow x.\tan {75^o} = \left( {x + 20} \right).\tan {35^o}\\ \Leftrightarrow x = \frac{{20.\tan {{35}^o}}}{{\tan {{75}^o} - \tan {{35}^o}}} \approx 4,6\end{array}\)
Suy ra OH = 26,1.
Vậy chiếc diều bay cao 26,1 m so với mặt đất.

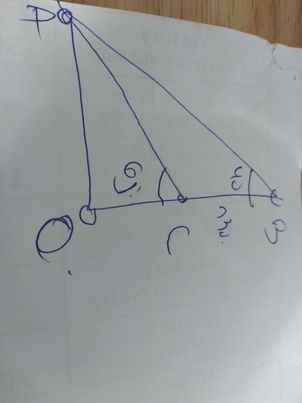
Kẻ AO vuông góc với BC tại O
=>OC là độ cao của ngọn đồi
\(\widehat{ACO}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+65^0=180^0\)
=>\(\widehat{ACB}=115^0\)
Xét ΔACB có \(\widehat{ACO}\) là góc ngoài tại C
nên \(\widehat{ACO}=\widehat{CAB}+\widehat{CBA}\)
=>\(\widehat{CAB}+40^0=65^0\)
=>\(\widehat{CAB}=25^0\)
Xét ΔCAB có
\(\dfrac{BA}{sinACB}=\dfrac{BC}{sinBAC}\)
=>\(\dfrac{BA}{sin115}=\dfrac{130}{sin25}\)
=>\(BA=\dfrac{130}{sin25}\cdot sin115\simeq278,79\left(m\right)\)
Xét ΔBOA vuông tại O có \(cosABO=\dfrac{BO}{BA}\)
=>\(\dfrac{BO}{278.79}=cos40\)
=>\(BO=278,79\cdot cos40\simeq213,57\left(m\right)\)
BO=BC+CO
=>CO+130=213,57
=>CO=83,57(m)
Vậy: Độ cao của ngọn đồi là 83,57 mét

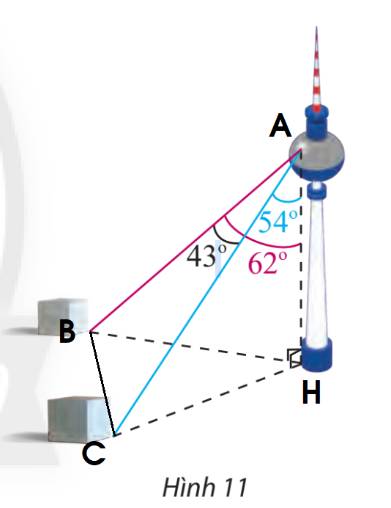
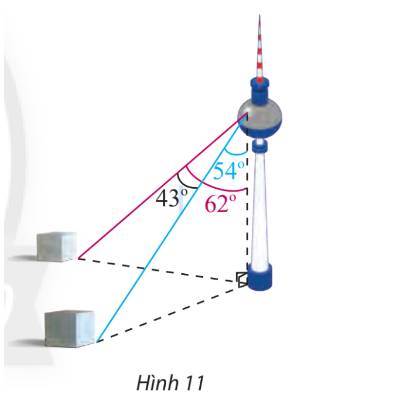
Gọi các điểm A, B, C, H như hình trên.
Xét tam giác ABH ta có:
\(AH = 352,\;\widehat {BAH} = {62^ \circ }\)
Mà \(\cos \widehat {BAH} = \frac{{AH}}{{AB}} \Rightarrow AB = 352 : \cos {62^ \circ } \approx 749,78\)
Tương tự, ta có: \(\cos \widehat {CAH} = \frac{{AH}}{{AC}} \Rightarrow AC = 352:\cos {54^ \circ } \approx 598,86\)
Áp dụng định lí cosin cho tam giác ABC, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {749,78^2} + {598,86^2} - 2.749,78.598,86.\cos {43^ \circ }\\ \Rightarrow BC \approx 513,84\end{array}\)
Vậy khoảng cách giữa hai cột mốc này là 513,84 m.

Tam giác ABC vuông tại B nên ta có: \(\tan C = \frac{{AB}}{{CB}} \Leftrightarrow AB = \tan {32^ \circ }.(1 + x)\)
Tam giác ADB vuông tại B nên ta có: \(\tan D = \frac{{AB}}{{DB}} \Leftrightarrow AB = \tan {40^ \circ }.x\)
\(\begin{array}{l} \Rightarrow \tan {32^ \circ }.(1 + x) = \tan {40^ \circ }.x\\ \Leftrightarrow x.(\tan {40^ \circ } - \tan {32^ \circ }) = \tan {32^ \circ }\\ \Leftrightarrow x = \frac{{\tan {{32}^ \circ }}}{{\tan {{40}^ \circ } - \tan {{32}^ \circ }}}\\ \Leftrightarrow x \approx 2,9\;(km)\end{array}\)
\( \Rightarrow AB \approx \tan {40^ \circ }.2,92 \approx 2,45\;(km)\)
Vậy chiều cao của ngọn núi là 2,45 km.

Khi đo độ cao đỉnh núi Everest người ta không thể đo trực tiếp một cách chính xác mà phải thông qua tính toán.
Mỗi vị trí quan sát hoặc trong tính toán, có những con số không thể lấy chính xác đo đó kết quả thu được cũng không giống nhau.
Ngoài ra có thể người ta đã làm tròn kết quả để được một con số gọn mà chính xác nhất có thể, nên các kết quả cũng khác nhau.
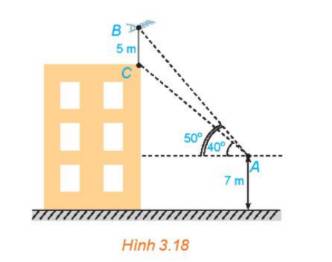



ve hinh thang vuong ABED co AD//BC ; va ED vuong goc voi BC keo dai ;
E thuoc BC keo dai(hinh chieu cua BC tren mat dat)
.D la diem duoi mat dat cua A AD=7m; BC=5m
Cac goc 40 ; 50 do la giua AC ; AB voi phuong nam ngang .
Ta tinh duoc DE theo BC : DE =BC/(tan50-tan40)
=> Bc da biet tan ta tra duoc .Con CE la chieu cao cua nha :
Vay : CE=AD+DE*tan40= 7+5*tan40/(tan50-tan40)