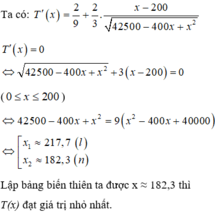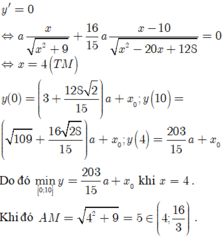Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Vận tốc của cá hồi khi bơi ngược là v–6(km/h).
Thời gian cá bơi để vượt khoảng cách 300km là: ![]()
Năng lượng tiêu hao của cá để vượt khoảng cách đó là:

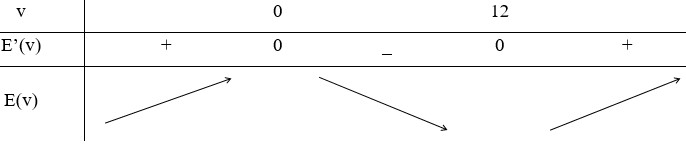
Để ít tiêu hao năng lượng nhất, cá phải bơi với vận tốc ( khi nước đứng yên) là 12(km/h).

Đáp án C.
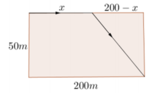
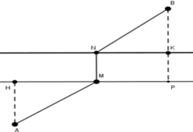
Gọi quãng đường vận động viên chạy trên bờ là x (m).
Khi đó quãng đường vận động viên bơi dưới nước sẽ là ![]()
Thời gian cho cả quãng đường đi (cả trên bờ và dưới nước) là
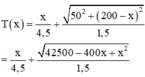
Yêu cầu bài toán tương đương với: tìm x để đạt giá trị nhỏ nhất.
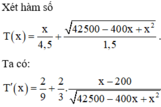
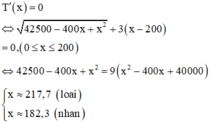
Lập bảng biến thiên ta được x ≈ 182 , 3 m thì T(x) đạt giá trị nhỏ nhất.

Đáp án C
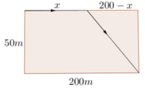
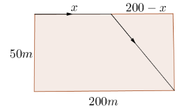
Gọi quãng đường vận động viên chạy trên bờ là x (m)
Khi đó quãng đường vận động viên đó bơi dưới nước sẽ là 50 2 + 200 − x 2 (m)
Thời gian cho cả quãng đường đi (cả trên bờ và dưới nước) là



Đáp án D
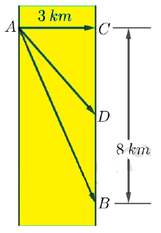
Thời gian đi từ A đến B là t A B = 3 2 + 8 2 6 = 73 6 h .
Thời gian đi từ A đến C rồi đến B là t A C B = 3 6 + 8 8 = 3 2 h
Gọi C D = x k m ⇒ t A D B = x 2 + 9 6 + 8 − x 8 h .
Xét hàm số f x = x 2 + 9 6 + 8 − x 8 0 ≤ x ≤ 8
f ' x = x 6 x 2 + 9 − 1 8 ⇒ f ' x = 0 ⇔ x = 9 7 .
Suy ra f 0 = 3 2 = t A C B , f 8 = 73 6 = t A B , f 9 7 = 1 + 7 8 .
Suy ra thời gian ngắn nhất bằng 1 + 7 8 h .

Đáp án D
Vận tốc của con cá khi bơi ngược dòng được là v - 3 (km/h)
Thời gian cá bơi được quãng đường 240km là ![]()
Năng lượng tiêu hao của cá để vượt quãng đường đó là 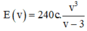
Bài toán trở thành tìm v>3 để E(v) là nhỏ nhất.
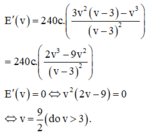
Vậy v=92 thỏa mãn đề bài.