Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hàm số y = f(x) = x4 - 3x2 + 1 có tập xác định D là R, do đó ∀ x ∈ D thì -x ∈ D, hơn nữa f(-x) = (-x)4 - 3(-x)2 + 1 = x4 - 3x2 + 1 = f(x), nên y = f(x) là hàm số chẵn.
b) Hàm số y = g(x) = -2x3 + x có tập xác định D là R, do đó ∀ x ∈ D thì -x ∈ D, hơn nữa g(-x) = -2(-x)3 + (-x) = 2x3 - x = -g(x), nên y = g(x) là hàm số lẻ.
c) Hàm số y = h(x) =|x + 2|- |x - 2 | có tập xác định D là R, do đó ∀ x ∈ D thì –x ∈ D, hơn nữa h(-x) = | -x + 2| -|-x – 2|= |x - 2| - |x + 2|= -(|x + 2| - |x - 2 |) = -h{x)
Vì vậy y = h(x) là hàm số lẻ.
d) Chứng minh tương tự ta có y = |2x + 1| + |2x — 1| là hàm số chẵn.

Đặt y = f(x) = x2 + x + 1.
+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
+ f(–x) = (–x)2 + (–x) + 1 = x2 – x + 1 ≠ x2 + x + 1 = f(x)
+ f(–x) = (–x)2 + (–x) + 1 = x2 – x + 1 ≠ –(x2 + x + 1) = –f(x)
Vậy hàm số y = x2 + x + 1 không chẵn, không lẻ.

Hàm số ở câu a) \(y = 9{x^2} + 5x + 4\) là hàm số bậc hai với \(a = 9,b = 5,c = 4\)
Hàm số ở câu b), c) không phải là hàm số bậc hai vì chứa \({x^3}\)
Hàm số ở câu d) \(y = 5{x^2} + \sqrt x + 2\) không phải là hàm số bậc hai vì chứa \(\sqrt x \)

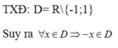
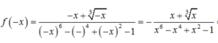
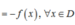

Lời giải:
Hàm số chẵn là hàm số được xác định như sau:
Với mọi $x\in D thì -x\in D$ và $f(x)=f(-x)$
Dựa vào định nghĩa này ta có thể thấy:
Với $x\in\mathbb{R}\Rightarrow -x\in\mathbb{R}$:
\(y(x)=|x^2-1|+x\)
\(y(-x)=|(-x)^2-1|+(-x)=|x^2-1|-x\)
Ta thấy việc $y(x)=y(-x)$ không xảy ra với mọi $x,-x\in\mathbb{R}$
Do đó hàm số ở phần $D$ không phải hàm chẵn