Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

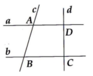
Ta có B A D ^ + A B C ^ = 180° => a // b
Mà B C D ^ = 90°=>d ⊥ b. Do đó d ⊥ a

a: góc B=góc C=(180-110)/2=35 độ
D nằm trên trung trực của AB
=>DA=DB
=>ΔDAB cân tại D
=>góc DAB=góc DBA=35 độ
E nằm trên trung trực của AC
=>EA=EC
=>góc EAC=góc ECA=35 độ
góc DAE=110-35-35=40 độ
b: 2*góc BAC=2*110=220 độ
góc DAE+180 độ=40 độ+180 độ=220 độ
=>2*góc BAC=góc DAE+180 độ

a, Vì m và n cùng vuông góc với a nên m//n
b, Vì m//n nên \(\widehat{B_1}=\widehat{D_1}=70^0\left(so.le.trong\right);\widehat{B_1}=\widehat{D_2}=70^0\left(đồng.vị\right)\)
c, Vì \(\widehat{B_1}+\widehat{G_1}=70^0+110^0=180^0\) mà 2 góc này ở vị trí trong cùng phía nên p//n
Mà n⊥a nên p⊥a

Mình làm tắt nha:
a, Ta có: tam giác ABD = tam giác AHD (ch+gn)
=>AB=AH
=> tam giác ABI = tam giác AHI (ch+cgv)
=> Góc AIB=góc AIH mà chúng kề bù
=> góc AIB = AIH = 900.
=> AH vuông góc với BD
b, tam giác ABD = tam giác AHD (cmt)
=> góc ADB=ADH mà tổng bằng 1100
=> góc ADB = ADH = 550.
=> góc DAH = 1800-900-550=350.
=> góc BAH = 900-350=550.

a) Xét ΔBAD có BA=BD(gt)
nên ΔBAD cân tại B(Định nghĩa tam giác cân)
Suy ra: \(\widehat{BAD}=\widehat{BDA}\)(hai góc ở đáy)
b) Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)(tia AD nằm giữa hai tia AB,AC)
\(\widehat{HAD}+\widehat{HDA}=90^0\)(ΔHAD vuông tại H)
mà \(\widehat{BAD}=\widehat{HDA}\)(cmt)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của \(\widehat{HAD}\)
c) Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)(AD là tia phân giác của \(\widehat{HAK}\))
Do đó: ΔAHD=ΔAKD(Cạnh huyền-góc nhọn)
Suy ra: AH=AK(hai cạnh tương ứng)
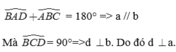
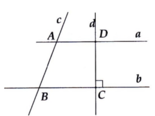
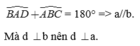
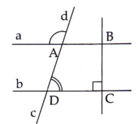
Ta có: \(\widehat{BAD}+\widehat{ABC}=110^o+70^o=180^o\)
Mà 2 góc này là 2 góc trong cùng phía ⇒a//b
a//b, b⊥d⇒a⊥d
Ta có \(\widehat{BAD}\) + \(\widehat{ABC}\) = 180° => a // b
Mà \(\widehat{BCD}\) = 90°=>d ⊥ b. Do đó d ⊥ a