Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 8 là \(\left(8a^2-\dfrac{1}{2}b\right)^6\) hay \(\left(8a^2-\dfrac{1}{2b}\right)^6\) bạn? (tốt nhất là bạn dùng tính năng gõ công thức toán để đăng đề, hoặc chụp hình gửi đề trực tiếp lên, hiện nay hoc24 đã cho đăng đề bằng hình ảnh)
9.
\(\left(x+8.x^{-2}\right)^9=\sum\limits^9_{k=0}C_9^kx^{9-k}.8^k.x^{-2k}=\sum\limits^9_{k=0}C_9^k8^kx^{9-3k}\)
Số hạng ko chứa x \(\Rightarrow9-3k=0\Rightarrow k=3\)
Số hạng đó là: \(C_9^3.8^3=...\)

Tổng 20 số hạng đầu là:
\(u_1\cdot\dfrac{1-q^{20}}{1-q}=3\cdot\dfrac{1-2^{20}}{1-2}=3\cdot\dfrac{2^{20}-1}{2-1}=3\cdot\left(2^{20}-1\right)\)
=>Chọn C

Chọn C
Ta có: 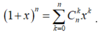 .
.
Số hạng tổng quát của khai triển là: ![]() . Hệ số của
x
k
trong khai triển là:
C
n
k
. Hệ số của
x
k
trong khai triển là:
C
n
k
Hệ số của số hạng chứa x 9 trong biểu thức P(x) là:
![]() .
.

Đáp án đúng là: A
Dãy số 21; – 3; – 27; – 51; – 75 lập thành một cấp số cộng có số hạng đầu là u1 = 21 và công sai d = – 24.

Bài 4:
\(u_n=5.\left(\frac{1}{2}\right)^{2n-1}=10.\left(\frac{1}{2}\right)^{2n}=10\left(\frac{1}{4}\right)^n\)
Là cấp số nhân với \(u_1=10\) và công bội \(q=\frac{1}{4}\)
Bài 5:
\(S_5=u_1.\frac{q^4-1}{q-1}=u_1.\frac{\left(\frac{1}{3}\right)^4-1}{\frac{1}{3}-1}=\frac{121}{81}u_1\)
\(\Rightarrow u_1=\frac{81}{121}S_5=81\)
Bài 6:
\(\left\{{}\begin{matrix}u_1q=4\\u_1q^3=9\end{matrix}\right.\) \(\Rightarrow\left(u_1q^2\right)^2=36\Rightarrow\left[{}\begin{matrix}u_1q^2=6\\u_1q^2=-6\end{matrix}\right.\)
Mà \(u_3=u_1q^2\Rightarrow u_3=\pm6\)
Bài 2:
\(\left\{{}\begin{matrix}u_1q^3-u_1q=24\\u_1q^2-u_1=12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1q\left(q^2-1\right)=24\\u_1\left(q^2-1\right)=12\end{matrix}\right.\)
\(\Leftrightarrow\frac{u_1q\left(q^2-1\right)}{u_1\left(q^2-1\right)}=\frac{24}{12}\Rightarrow q=2\Rightarrow u_1=\frac{12}{q^2-1}=4\)
\(\Rightarrow S_8=u_1.\frac{q^8-1}{q-1}=4\left(2^8-1\right)=...\)
Câu 3:
\(u_{10}=u_1q^9=4\left(-2\right)^9=-2^{11}\)
\(S_{15}=u_1.\frac{q^{15}-1}{q-1}=4.\frac{\left(-2\right)^{15}-1}{-3}=\frac{3}{4}\left(2^{15}+1\right)\)

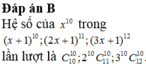
Ta có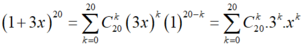
Số hạng đứng chính giữa ứng với k=10.
Suy ra hệ số của số hạng đứng chính giữa là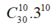 .
.
Chọn D.