

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



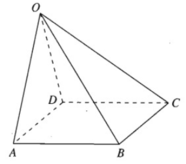
Giả sử bốn điểm A, B, C, D tạo thành một hình bình hành ta có:
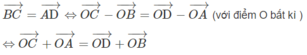
Ngược lại, giả sử ta có hệ thức:
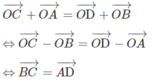
Vì A, B, C, D không thẳng hàng nên tứ giác ABCD là hình bình hành.

+) Trước hết, điều kiện cần và đủ để tứ giác ABCD là hình bình hành là: 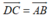 .
.
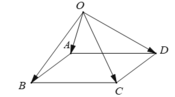
+) Với mọi điểm O bất kì khác A, B, C, D ta có:
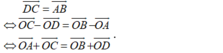
- Vậy điều kiện cần và đủ để tứ giác ABCD là hình bình hành là:
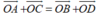

Chọn B.
- Trước hết, điều kiện cần và đủ để tứ giác ABCD là hình bình hành là:
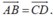
- Với mọi điểm O bất kì khác A, B, C, D ta có:
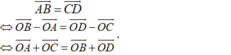

Gọi D là trung điểm BC và G là trọng tâm tam giác ABC
Theo tính chất trọng tâm: \(AG=\dfrac{2}{3}AD\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|=\left|\overrightarrow{MA}+\overrightarrow{BM}+\overrightarrow{MA}+\overrightarrow{CM}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right|=\left|\overrightarrow{BA}+\overrightarrow{CA}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MG}\right|=\left|-2\overrightarrow{AD}\right|\)
\(\Leftrightarrow MG=\dfrac{2}{3}AD=AG\)
\(\Rightarrow\) Tập hợp M là mặt cầu tâm G bán kính AG với G là trọng tâm tam giác ABC