

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đáp án B.
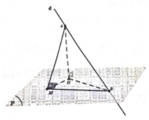
Gọi H là hình chiếu vuông góc của A lên mặt phẳng (P)
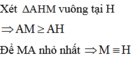
⇒ M B là giao tuyến của mặt phẳng (P) với mặt phẳng α ( α là mặt phẳng chứa d và vuông góc với mặt phẳng (P))
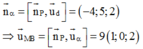
Vậy phương trình đường thẳng MB:
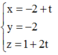
Thấy ngay điểm I(-1;-2;3) thỏa mãn.

PT đường thẳng d: \(\frac{x-1}{3}=\frac{y-2}{4}=\frac{z+3}{-3}\). Vì B \(\in\)d => \(B\left(3b+1;4b+a;-4b-3\right)\)
Mà B giao d tại P => 2(3b+1)+2(4a+2)+4b+3+9=0
<=> b=-1 => B(-2;-2;1)
Gọi A' là hình chiếu của A trên (P) => AA': \(\frac{x-1}{2}=\frac{y-2}{2}=\frac{z+3}{-1}\Rightarrow A\left(-3;-2;-1\right)\)
Theo bài ra ta có: MA2+MB2=AB2 <=> AB2-MA2 \(\le AB^2-AA'^2=A'B^2\)
Độ dài MB lớn nhất khi M trung với A': \(\hept{\begin{cases}x=-2+t\\y=-2\\z=1+2t\end{cases}\Rightarrow I\left(-1;-2;3\right)\in MB}\)

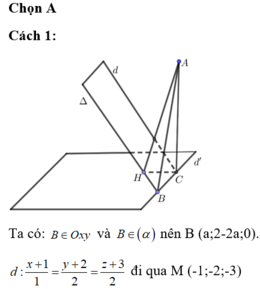
Ta có: d ⊂ (α) nên d và ∆ song song với nhau và cùng nằm trong mặt phẳng (α).
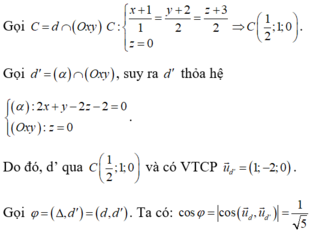



a. Mặt phẳng (P) có (3;-2;2) là 1 vtpt nên d nhận (3;-2;2) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=1+3t\\y=2-2t\\z=-1+2t\end{matrix}\right.\)
b. \(\overrightarrow{n_{\left(P\right)}}=\left(1;1;1\right)\) ; \(\overrightarrow{n_{\left(P'\right)}}=\left(1;-1;1\right)\)
\(\left[\overrightarrow{n_{\left(P\right)}};\overrightarrow{n_{\left(P'\right)}}\right]=\left(2;0;-2\right)=2\left(1;0;-1\right)\)
\(\Rightarrow\) d nhận (1;0;-1) là 1 vtcp nên pt có dạng: \(\left\{{}\begin{matrix}x=1+t\\y=-2\\z=3-t\end{matrix}\right.\)
c. \(\overrightarrow{u_{\Delta}}=\left(3;2;1\right)\) ; \(\overrightarrow{u_{\Delta'}}=\left(1;3;-2\right)\)
\(\left[\overrightarrow{u_{\Delta}};\overrightarrow{u_{\Delta'}}\right]=\left(-7;7;7\right)=7\left(-1;1;1\right)\)
Đường thẳng d nhận (-1;1;1) là 1 vtcp nên pt có dạng: \(\left\{{}\begin{matrix}x=-1-t\\y=1+t\\z=3+t\end{matrix}\right.\)