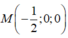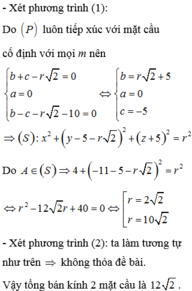
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


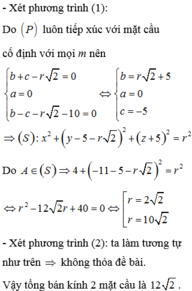

Chọn A
Điểm M(1;0;0) là 1 điểm thuộc (P)
Vì (P) // (Q) nên
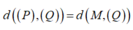
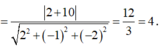
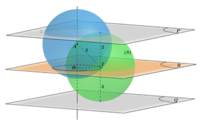
Giả sử I(a;b;c) là tâm của (S). Vì (S) tiếp xúc với cả (P) và (Q) nên bán kính mặt cầu (S) là:
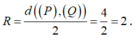
Do đó IA = 2 nên I luôn thuộc mặt cầu (T) tâm A, bán kính 2.
Ngoài ra
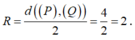
![]()
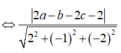
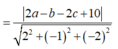
![]()
![]()
![]()
Do đó I luôn thuộc mặt phẳng (R): 2x-y-2z+4=0.
Gọi H là hình chiếu vuông góc của A lên (R). Vì A, (R) cố định nên H cố định.
Ta có
![]()
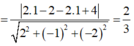
![]()
do đó tam giác AHI vuông tại H nên
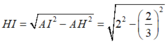
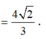
Vậy I luôn thuộc đường tròn tâm H, nằm trên mặt phẳng (R), bán kính
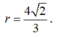

Đáp Án A
Gọi O là hình chiếu của A lên mp (P)
Ta có ptAO: x = 4 + t y = 6 + t z = 2 + t
⇒ t=-4 ⇒ O(0,2;-2)
Có HB ⊥ AO; HB ⊥ HA ⇒ HB ⊥ (AHO)
⇒ HB ⊥ HO
Ta có B;O cố định
Suy ra H nằm trên đường tròng đường kính OB cố định
⇒ r= 1 2 OB= 6

Chọn A
Cách 1:
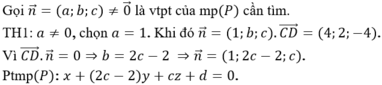

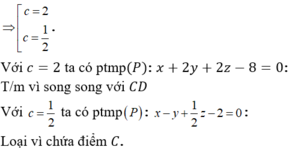

Cách 2: Ta có 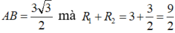 nên hai mặt cầu cắt nhau theo một đường tròn giao tuyến.
nên hai mặt cầu cắt nhau theo một đường tròn giao tuyến.
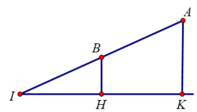
Gọi I = AB ∩ (α) với (α) là mặt phẳng thỏa mãn bài toán.
Hạ vuông góc với mặt phẳng .
Khi đó ta có I nằm ngoài AB và B là trung điểm AI vì
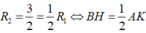
Suy ra I (2;1;2). Gọi (α): a(x-2) + b(y-1) + c(z-2) = 0.
Vì (α) // CD mà ![]() nên ta có 2a + b - 2c = 0 => b = 2c - 2a
nên ta có 2a + b - 2c = 0 => b = 2c - 2a
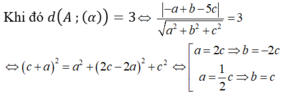
Ta có hai trường hợp:
Nếu b = -2c; a = 2c => (α): 2c (x-2) + 2c (y-1) + c(z-2) = 0 => 2x - 2y + z - 4 = 0
Mặt khác CD // (α) nên CD ∉ (α) loại trường hợp trên.
Nếu b = c; a = c/2 => (α): c/2 . (x-2) + c (y-1) + c(z-2) = 0 => x + 2y + 2z - 8 = 0
Kiểm tra thấy CD ∉ (α) nên nhận trường hợp này. Vậy (α): x + 2y + 2z - 8 = 0

Chọn A
Gọi ![]() là một vec tơ pháp tuyến của mặt phẳng (P).
là một vec tơ pháp tuyến của mặt phẳng (P).
Theo đề bài ta có mặt phẳng (P) vuông góc với mặt phẳng (α): x-y+z-4=0 nên ta có phương trình a-b+c=0 ó b=a+c ![]()
Phương trình mặt phẳng (P) đi qua A(0;1;2) và có véc tơ pháp tuyến là ax+ (a+c) (y-1)+c (z-2) =0
Khoảng cách từ tâm I (3;1;2) đến mặt phẳng (P) là 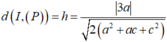
Gọi r là bán kính của đường tròn giao tuyến giữa mặt cầu (S) và mặt phẳng (P) ta có r²=16-h² ; r nhỏ nhất khi h lớn nhất.
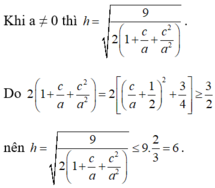
Dấu “=” xảy ra khi a = -2c. => một véc tơ pháp tuyến là ![]() => phương trình mặt phẳng (P) là 2x+y-z+1=0.
=> phương trình mặt phẳng (P) là 2x+y-z+1=0.
Vậy tọa độ giao điểm M của (P) và trục x'Ox là: