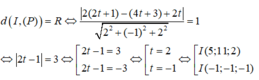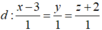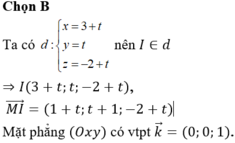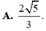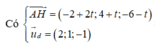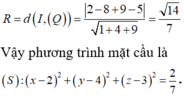Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B.
Phương pháp giải: Gọi tọa độ điểm, tính khoảng cách và tìm tọa độ tâm thông qua bán kính
Lời giải: Ta có
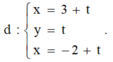
Phương trình mặt phẳng (Oxy): z=0
Khoảng cách từ tâm I đến mp(Oxy) là
Theo bài ra, ta có
Chọn A
Cách 1:
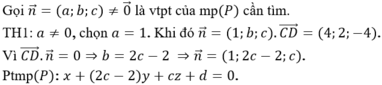
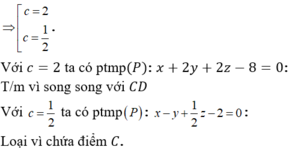
Cách 2: Ta có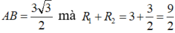 
nên hai mặt cầu cắt nhau theo một đường tròn giao tuyến.
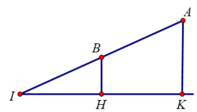
Gọi I = AB ∩ (α) với (α) là mặt phẳng thỏa mãn bài toán.
Hạ vuông góc với mặt phẳng .
Khi đó ta có I nằm ngoài AB và B là trung điểm AI vì
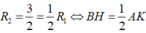
Suy ra I (2;1;2). Gọi (α): a(x-2) + b(y-1) + c(z-2) = 0.
Vì (α) // CD mà 
nên ta có 2a + b - 2c = 0 => b = 2c - 2a
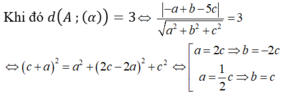
Ta có hai trường hợp:
Nếu b = -2c; a = 2c => (α): 2c (x-2) + 2c (y-1) + c(z-2) = 0 => 2x - 2y + z - 4 = 0
Mặt khác CD // (α) nên CD ∉ (α) loại trường hợp trên.
Nếu b = c; a = c/2 => (α): c/2 . (x-2) + c (y-1) + c(z-2) = 0 => x + 2y + 2z - 8 = 0
Kiểm tra thấy CD ∉ (α) nên nhận trường hợp này. Vậy (α): x + 2y + 2z - 8 = 0
Đáp án D
Phương trình tham số của đường thẳng d là : d: x = 1 +2 t, y = 3+ 4t, z = t
Ta có I ∈ d => I(1 + 2t, 3 + 4t, t). Vì (S) tiếp xúc với mặt phẳng (P) nên ta có:
