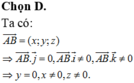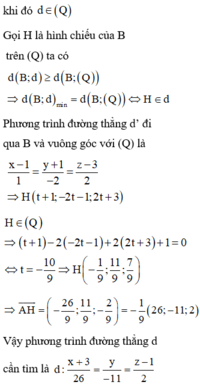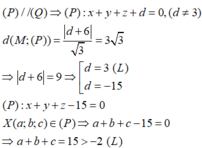Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Phương pháp :
Đường thẳng qua A song song với hai mặt phẳng (P); (Q) nhận 
là 1VTCP.
Cách giải : Ta có 
lần lượt là các VTPT của
Ta có :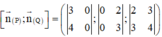
là 1 VTCP của đường thẳng qua A và vuông góc với cả
Vậy phương trình đường thẳng cần tìm là: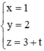 
Với t = -3 ta có đường thẳng đi qua điểm B(1;2;0) => phương trình đường thẳng cần tìm là :
x = 1 y = 2 z = t
Đáp án C
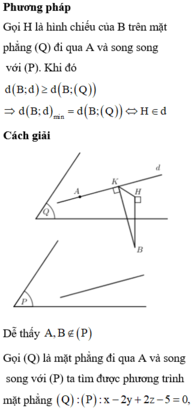
Gọi (Q) là mặt phẳng qua A và song song với
P ⇒ Q : x + y + 2 z − 4 = 0
Ta có d B ; d ≤ A B ⇒ d B , d max ⇔ AB ⊥ d.
Ta có A B ¯ = 1 ; − 1 ; 0 ⇒ u d ¯ = A B ¯ , n p ¯ = − 2 ; − 2 ; 2
Do đó phương trình đường thẳng d là d : x − 2 1 = y − 2 1 = z − 1 .
Chọn đáp án C
Mặt phẳng (P) có vectơ pháp tuyến là n 1 ⇀ = 2 ; a ; 3 ; mặt phẳng (Q) có vectơ pháp tuyến là n 2 ⇀ = b ; - 6 ; - 6 .
Để (P)//(Q) thì n 1 ⇀ , n 2 ⇀ cùng phương hay n 1 ⇀ = k n 2 ⇀
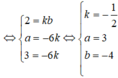
Đáp án D
Phương pháp :
Gọi (Q): x + y + z + a = 0 (a≠3) là mặt phẳng song song với mặt phẳng (P).
Sử dụng công thức tính khoảng cách từ 1 điểm đến một mặt phẳng.
Cách giải :
Gọi (Q): x + y + z + a = 0 (a≠3) là mặt phẳng song song với mặt phẳng (P).
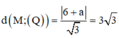
Với 
Vậy không có mặt phẳng (Q) nào thỏa mãn điều kiện bài toán