Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Mặt cầu S 1 có tâm M(2;1;0) và có bán kính R 1 = 1
Gọi M' là hình chiếu vuông góc của M trên mặt phẳng (Q)
Ta có M M ' ⊥ Q nên đường thẳng MM' đi qua điểm M và nhận vectơ pháp tuyến của mặt phẳng (Q) làm vectơ chỉ phương.
=> phương trình tham số đường thẳng MM': x = 2 + 2 t y = 1 − 2 t z = − t , t ∈ ℝ
Vì M' là hình chiếu vuông góc của M trên mặt phẳng Q ⇒ M ' = M M ' ∩ Q
=> tọa độ điểm M' là nghiệm hệ phương trình:
2 x − 2 y − z + 1 = 0 x = 2 + 2 t y = 1 − 2 t z = − t ⇔ 2 2 + t − 2 1 − 2 t − − t + 1 = 0 x = 2 + 2 t y = 1 − 2 t z = − t ⇔ t = − 1 3 x = 4 3 y = 5 3 z = 1 3
⇒ M ' 4 3 ; 5 3 ; 1 3
Gọi I(x;y;z) là tâm của mặt cầu (S'), do mặt cầu (S') đối xứng với mặt cầu (S) qua mặt phẳng (Q) => I đối xứng với M qua mặt phẳng (Q)
=> I đối xứng với M qua mặt phẳng M'
=> M' là trung điểm của đường thẳng IM.
⇒ x = 2 x M ' − x M = 2 3 y = 2 y M ' − y M = 7 3 z = 2 z M ' − z M = 2 3 ⇒ I 2 3 ; 7 3 ; 2 3
Khi đó mặt cầu (S') có tâm I 2 3 ; 7 3 ; 2 3 , bán kính R' = R = 1 nên có phương trình:
x − 2 3 2 + y − 7 3 2 + z − 2 3 2 = 1

Chọn C.
Phương pháp: Lần lượt tìm các yếu tố tâm và bán kính của mặt cầu.
Cách giải: Tọa độ tâm mặt cầu thỏa mãn hệ


Đáp án C.
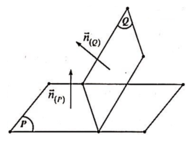
Mặt phẳng (Q) có vectơ pháp tuyến n → 2 ; − 2 ; − 1
Mặt cầu (S) tâm M và tiếp xúc với mặt phẳng (Q) nên có bán kính R = d M , Q = 2.2 + 2 + 1 4 + 4 + 1 = 7 3
Phương trình mặt cầu S : x − 2 2 + y − 1 2 + z 2 = 49 9

Đáp án D
Mặt cầu (S) có tâm I 1 ; − 2 ; 0 và bán kính R = 21
Đường thẳng Δ 1 có vtcp u 1 → = 2 ; − 3 ; 2 và đường thẳng Δ 2 có vtcp u 2 → = 1 ; 1 ; − 1
Mặt phẳng α có vtcp n → = u 1 → , u 2 → = 1 ; 4 ; 5 ⇒ α : x + 4 y + 5 z + m = 0
Do tiếp xúc với mặt cầu (S) nên
d I , α = 21 ⇔ 1 + 4. − 2 + 5.0 + m 1 2 + 4 2 + 5 2 = 21 ⇔ m = 7 + 21 2 m = 7 − 21 2
Do α cắt trục Oz tại điểm có cao độ dương ta có phương trình của α : x + 4 y + 5 z + 7 − 21 2 = 0


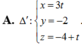

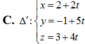
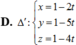



Đáp án là A.
+ Mặt phẳng chứa Ox có dạng B y + C z = 0
+ Do mặt cầu tiếp xúc với mặt phẳng nên:
2 B − C B 2 + C 2 = 1 ⇔ B = 0 B = 4 , C = 3
Vậy mặt phẳng cần tìm 4 y + 3 z = 0