Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải
Vì 3 điểm A, B, C thuộc các trục Ox, Oy, Oz nên ta giả sử tọa độ của ba điểm lần lượt là A(a;0;0), B (0;b;0), C (0;0;c)
Khi đó mặt phẳng (P) có dạng: \(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\)
Ta có: 3OA = 2OB = OC khác 0 nên suy ra:
a, b, c khác 0
3 |a| = 2 |b| (1)
3 |a| = |c| (2)
Điểm M (-1;0;3) thuộc (P) nên ta có: \(\dfrac{-1}{a}+\dfrac{3}{c}=1\left(3\right)\)
Từ (2) suy ra c = 3a hoặc c = -3a.
Thay c = 3a vào (3) ta có \(-\dfrac{1}{a}+\dfrac{1}{a}=1\) ( vô nghiệm)
Thay c = -3a vào (3) ta có \(-\dfrac{1}{a}-\dfrac{1}{a}=1\Leftrightarrow\dfrac{-2}{a}=1\Leftrightarrow a=-2\)
Suy ra c = 6, b = 3 hoặc c = 6, b = -3
Vậy ta có hai phẳng (P) là: \(\dfrac{x}{-2}+\dfrac{y}{3}+\dfrac{z}{6}=1\) hoặc \(\dfrac{x}{-2}+\dfrac{y}{-3}+\dfrac{z}{6}=1\) .

Câu 1:
Do \(MA=MB\Rightarrow M\) là trung điểm AB
Gọi \(B\left(a;0;0\right)\) \(\Rightarrow\left\{{}\begin{matrix}x_A=2x_M-x_B=6-a\\y_A=2y_M-y_B=4\\z_A=2z_M-z_B=2\end{matrix}\right.\)
Mà \(A\in\left(Q\right)\)
\(\Rightarrow6-a+4+2-7=0\Rightarrow a=5\)
\(\Rightarrow\left\{{}\begin{matrix}B\left(5;0;0\right)\\A\left(1;4;2\right)\end{matrix}\right.\) \(\Rightarrow AB=6\)
Câu 2:
Gọi (Q) là mặt phẳng chứa A và song song (P)\(\Rightarrow d\in\left(Q\right)\)
Phương trình (Q):
\(2\left(x-1\right)+1\left(y-2\right)-4\left(z-3\right)=0\)
\(\Leftrightarrow2x+y-4z+8=0\)
Giao điểm B của (Q) và trục Ox: \(2x+8=0\Rightarrow x=-4\) \(\Rightarrow B\left(-4;0;0\right)\)
\(\Rightarrow d\) nhận \(\overrightarrow{u_d}=\overrightarrow{BA}=\left(5;2;3\right)\) là một vtcp
Phương trình d: \(\left\{{}\begin{matrix}x=-4+5t\\y=2t\\z=3t\end{matrix}\right.\)

Đáp án D
Ta có: OA → OB, OC => OA → (OBC) => OA → BC
Mặt khác vì AM → BC (M là trực tâm tam giác ABC) nên ta suy ra BC → (OAM) => BC → OM
Chứng minh tương tự ta được AC → OM. Do đó OM → (ABC). Ta chọn: n p → = OM → = (1; -2; 3)
Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) - 2(y + 2) + 3(z - 3) = 0 ⇔ x - 2y + 3z - 14 = 0

Đáp án C
Phương pháp
+) Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a, b, c ≠ 0) viết phương trình mặt phẳng (P) đi qua A, B, C dạng đoạn chắn.M ∈ (P)=> Thay tọa độ điểm M vào phương trình mặt phẳng (P).
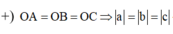
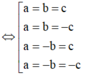
+) Ứng với mỗi trường hợp tìm các ẩn a, b, c tương ứng
Cách giải
Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a, b, c ≠ 0) khi đó phương trình mặt phẳng đi qua A, B, C là
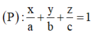
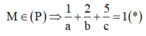
![]()
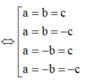
TH1: a=b=c thay vào (*) có
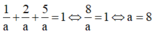
![]()
TH2: a=b=-c thay vào (*) có
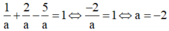
![]()
TH3: a=-b=c thay vào (*) có
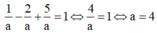
![]()
TH4: a=-b=-c thay vào (*) có
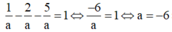
![]()
Vậy có 4 mặt phẳng thỏa mãn.
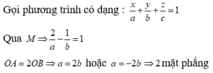

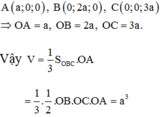
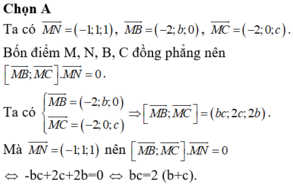
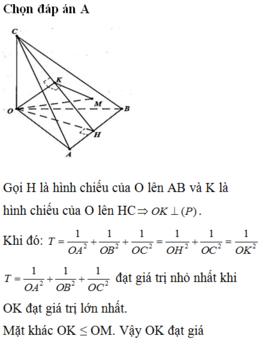

Chọn B
Gọi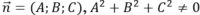 là vectơ pháp tuyến của (P) thỏa yêu cầu bài toán.
là vectơ pháp tuyến của (P) thỏa yêu cầu bài toán.
(P) qua N (-1; 0; -1) nên phương trình mặt phẳng có dạng:
A(x+1) + By + C(z+1) = 0 <=> Ax + By + Cz + A + C = 0
• (P) qua M (1;2;1) suy ra
A + 2B + C + A + C = 0 <=> A + B + C = 0 => A + C = - B (1)
• (P) cắt trục Ox tại A(a; 0; 0) suy ra A.a + A + C = 0 => A.a - B = 0 => a = B/A
(Do nếu A = 0 => B = 0 => C = 0 nên A ≠ 0). Suy ra A(B/A; 0; 0)
• (P) cắt trục Oy tại B (0; b; 0) suy ra B.b + A + C = 0 => B.b - B = 0 => B = 0 hoặc b = 1
TH1: B = 0 => A + C = 0. Chọn C = 1 => A = -1
Phương trình mặt phẳng (P) có dạng: x - z = 0 => A ≡ B ≡ O (0;0;0) => không thỏa yêu cầu.
TH2: b = 1 => B (0;1;0),
· B/A = -1 => B = -A => C = 0. Chọn A = 1 => B = -1
Phương trình mp (P): x - y + 1 = 0
· B/A = 3 => B = 3A => C = -4A. Chọn A = 1 => B = 3 => C = -4.
Phương trình mp (P): x + 3y - 4z - 3 = 0
Vậy có hai mặt phẳng thỏa yêu cầu.