Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: vecto AB=(2;-1)
PTTS AB là:
x=1+2t và y=2-t
vecto AB=(2;-1)
=>VTPT là (1;2)
PTTQ của AB là:
1(x-1)+2(y-2)=0
=>x-1+2y-4=0
=>x+2y-5=0
c:PT đường cao CH là:
2(x-5)+(-1)(y-4)=0
=>2x-10-y+4=0
=>2x-y-6=0
Tọa độ hình chiếu của C trên AB là:
2x-y-6=0 và x+2y-5=0
=>C(17/5;4/5)
e: PT (C) có dạng là:
x^2+y^2-2ax-2by+c=0
Theo đề, ta có:
1+4-2a-4b+c=0 và 9+1-6a-2b+c=0 và 25+16-10a-8b+c=0
=>a=23/8; b=13/4; c=55/4
=>(C): x^2+y^2-23/4x-13/2x+55/4=0
=>x^2-2*x*23/8+529/64+y^2-2*x*13/4+169/16=325/64
=>(x-23/8)^2+(y-13/4)^2=325/64

AB vuông góc CH nên nhận \(\left(1;1\right)\) là 1 vtpt
Phương trình AB:
\(1\left(x-1\right)+1\left(y-2\right)=0\Leftrightarrow x+y-3=0\)
B là giao điểm BN và AB nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}2x+y+5=0\\x+y-3=0\end{matrix}\right.\) \(\Rightarrow B\left(-8;11\right)\)
Gọi D là điểm đối xứng A qua BN \(\Rightarrow D\in BC\)
Phương trình đường thẳng d qua A và vuông góc BN (nên nhận \(\left(1;-2\right)\) là 1 vtpt) có dạng:
\(1\left(x-1\right)-2\left(y-2\right)=0\Leftrightarrow x-2y+3=0\)
Gọi E là giao điểm d và BN \(\Rightarrow E\) là trung điểm AD
Tọa độ E là nghiệm: \(\left\{{}\begin{matrix}2x+y+5=0\\x-2y+3=0\end{matrix}\right.\) \(\Rightarrow E\left(-\dfrac{13}{5};\dfrac{1}{5}\right)\)
\(\Rightarrow D\left(-\dfrac{31}{5};-\dfrac{8}{5}\right)\Rightarrow\overrightarrow{BD}=\left(\dfrac{9}{5};-\dfrac{63}{5}\right)=\dfrac{9}{5}\left(1;-7\right)\)
\(\Rightarrow\) Đường thẳng BC nhận (7;1) là 1 vtpt
Phương trình BC:
\(7\left(x+8\right)+1\left(y-11\right)=0\Leftrightarrow7x+y+45=0\)

AB=căn (5-1)^2+(2-2)^2=4
AC=căn (1-1)^2+(-3-2)^2=5
BC=căn (1-5)^2+(-3-2)^2=căn 41
AB^2+AC^2=BC^2
=>ΔABC vuông tại A
=>R=BC/2=căn 41/2 và tâm I là trung điểm của BC
Tọa độ I là;
x=(5+1)/2=3 và y=(2-3)/2=-1/2
Phương trình đường tròn là:
(x-3)^2+(y+1/2)^2=41/4

Gọi (C): x^2+y^2-2ax-2by+c=0 là PT đường tròn ngoại tiêpΔACB
Theo đề, ta có:
2^2+(-1)^2-4a+2b+c=0 và 1+4+2a-4b+c=0 và 16+1+8a+2b+c=0
=>-4a+2b+c=-5 và 2a-4b+c=-5 và 8a+2b+c=-17
=>a=-1; b=-1; c=-7
=>x^2+y^2+2x+2y-7=0
=>x^2+2x+1+y^2+2y+1=9
=>(x+1)^2+(y+1)^2=9

a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC
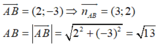
Phương trình tổng quát của AB là: 3(x - 1) + 2(y - 2) = 0 ⇔ 3x + 2y - 7 = 0
Kẻ CH ⊥ AB, (H ∈ AB)
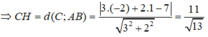
Diện tích tam giác ABC là:
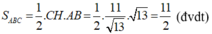
b) Viết phương trình đường tròn đường kính AB
Gọi I là trung điểm của AB
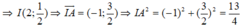
Đường tròn đường kính AB là đường tròn tâm I bán kính IA:
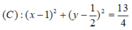

a: (d): 2x-y+3=0
=>y=2x+3
Vì (d') vuông góc với (d) nên 2a=-1
=>a=-1/2
Vậy: (d'): y=-1/2x+b
Thay x=3 và y=1 vào (d'), ta được:
b-3/2=1
hay b=5/2
Vậy: (d'): y=-1/2x+5/2
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x+3=-\dfrac{1}{2}x+\dfrac{5}{2}\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{2}x=-\dfrac{1}{2}\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{5}\\y=-\dfrac{2}{5}+3=\dfrac{13}{5}\end{matrix}\right.\)

Gọi M là trung điểm AB
=> IM vuông góc AB
Ta có: AM = MB = AB : 2 = 4 cm
IM = d( I; d) = \(\frac{3.1+4.2+4}{\sqrt{3^2+4^2}}=3\) cm
Tam giác IMA vuông tại M
=> R = IA = \(\sqrt{3^2+4^2}=5\)
=> Phương trình đường tròn cần tìm: ( x - 1)^2 + ( y - 2)^2 = 25
\(\overrightarrow{AB}=\left(3;-4\right)\Rightarrow AB=5\) ; \(\overrightarrow{CA}=\left(4;-3\right)\Rightarrow AC=5\)
\(\Rightarrow AB=AC\Rightarrow\) tam giác ABC cân tại A
\(\Rightarrow\) Phân giác trong góc A đồng thời là trung tuyến ứng với BC
Gọi M là trung điểm BC \(\Rightarrow M\left(\dfrac{1}{2};\dfrac{3}{2}\right)\Rightarrow\overrightarrow{MA}=\left(\dfrac{1}{2};\dfrac{1}{2}\right)=\dfrac{1}{2}\left(1;1\right)\)
\(\Rightarrow\) Đường thẳng AM nhận (1;-1) là 1 vtpt
Phương trình AM (đồng thời là phân giác trong góc A):
\(1\left(x-1\right)-1\left(y-2\right)=0\Leftrightarrow x-y+1=0\)