Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a. Phương trình đường tròn : (x – 3)2 + (y + 2)2 = 9.
b. (I1; R1) là ảnh của (I; 3) qua phép tịnh tiến theo vec tơ v.
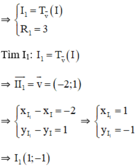
⇒ Phương trình đường tròn cần tìm: (x – 1)2 + ( y + 1)2 = 9.
c. (I2; R2) là ảnh của (I; 3) qua phép đối xứng trục Ox
⇒ R2 = 3 và I2 = ĐOx(I)
Tìm I2: I2 = ĐOx(I) ⇒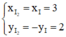 
⇒ I2(3; 2)
⇒ Phương trình đường tròn cần tìm: (x – 3)2 + (y – 2)2 = 9.
d. (I3; R3) là ảnh của (I; 3) qua phép đối xứng qua gốc O.
⇒ R3 = 3 và I3 = ĐO(I)
Tìm I3: I3 = ĐO(I) ⇒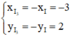 
⇒ Phương trình đường tròn cần tìm: (x + 3)2 +(y – 2)2 = 9.
Câu 1:
Lấy $M(x,y)\in (d)$. $M'(x',y')=T_{\overrightarrow{v}}(M)$
\(\left\{\begin{matrix} x'-x=2\\ y'-y=-1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=x'-2\\ y=y'+1\end{matrix}\right.\)
Ảnh của $d$ qua phép tịnh tiến theo vecto $\overrightarrow{v}$ có dạng:
$3(x'-2)-2(y'+1)+1=0$
$\Leftrightarrow 3x'-2y'-7=0$
Câu 2:
$M(x,y)$ là 1 điểm thuộc đường tròn $(C)$.
Lấy $M'(x',y')$ là 1 điểm thuộc $(C')$ là ảnh của $(C)$ qua $\overrightarrow{v}$
Khi đó, $M'=T_{\overrightarrow{v}}(M)
\(\Rightarrow \left\{\begin{matrix} x'-x=-3\\ y'-y=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=x'+3\\ y=y'-5\end{matrix}\right.\)
PTĐTr $(C')$ có dạng:
$(x'+3)^2+(y'-5)^2-4(x'+3)+6(y'-5)+5=0$
$\Leftrightarrow x'^2+y'^2+2x'-4y'-3=0$
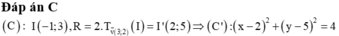
(C): (x - 2)2 + (y - 1)2 = 16
=> R=4 là bán kính (C) và I(2,1) là tâm của (C)
T\(\overrightarrow{v}\) (C) --->(C') => R'=4 là tâm (C') và T\(\overrightarrow{v}\) I(2,1) --->I'(2+1,1+2)=(3,3) là tâm của (C')
Vậy (C'): (x-3)2+(y-3)2=16