người thứ 2 nói lúc đó hắn thấy cờ treo lộn ngược nên trèo lên chỉnh lại, cờ ngược của vn lộn lại vẫn giống nhau nên hắn là thủ phạm

Người thứ 2 là thủ phạm bởi cờ VN xuôi hay hay ngược thì cx giống nhau .

Oa ! Chúc mừng bạn được 1 vé bào cáo VIP nek, sướng quá nhỉ???

Giôn là thủ phạm.

theo mình nghĩ thì ng` thứ nhất có số bàn thắng nhìu hơn 1 trong 2 ng` còn lại thì số bàn thắng ít nhất phải là 2 bàn. Ng`  thứ hai lại nói tôi có số bàn thua ít nhất trong 3 ng` chơi thì số bàn thua ít nhất phải là 1 vì họ ko nói là ko có thua vì vậy phải là ít nhất 1 bàn mới đúng và họ yêu cầu chúng ta tìm ng` thứ 3 có nhìu điểm nhất đúng hay ko thì:

Giải:

Gọi 3 ng` chơi lần lượt là a, b, c

Ta có:

a trên 2 = b trên 1 = c trên 0 suy ra a - b + c trên 2 - 1 + 0 = 1 vì thua là âm mà thắng là dương nên thay vào là + và - nha

a trên 2 = 1 thì suy ra 1 nhân với a chia cho 2 = 0,5

b trên 1 = 1 thì suy ra 1 nhân  với b chia cho 1 = 1

c trên 0 = 1 thì suy ra 1 nhân   với c chia cho 0 = 1

vậy ng` thứ 3 có số điểm cao nhất là sai vì ng` thứ 2 và 3 đều đc 1 điểm

còn biết rằng cứ 2 ng` chơi với nhau 1 số ván như sau có nghĩa là cứ 2 ng` sẽ chơi với nhau 1 hoặc 2 ván vậy đó nhưng theo mình thì ở đây hơi mập mờ giống như đề bài bị thiếu vậy ho nên mình ko chắc là mình có làm đúng hay ko đâu

hòa đc tihs điểm ko vậy

Còn về Pythagoras Triples, có những bộ số nguyên dương được gọi là bộ ba Pythagoras sẽ luôn đúng khi áp dụng vào công thức của Pythagoras như : 3^2 4^2 = 5^2; 8^2 15^2 = 17^2. Chúng được gọi là Bộ Ba Số Nguyên Dương Pythagoras.

Và bạn hãy tưởng tượng rằng mọi số nguyên dương trong bảng chữ số sẽ được tô màu hoặc đỏ hoặc xanh. Graham đã đưa ra bài toán rằng: liệu có khả thi không khi thực hiện việc tô màu mọi số nguyên hoặc xanh hoặc đỏ, để cho không có Bộ Ba Pythagoras nào có cùng màu. Và 100 USD sẽ được thưởng cho bất cứ người nào giải được bài toán ấy (Chà, với 100 USD thì ta có thể chi trả cho tận 1 cái ổ có dung lượng 1 terabyte).

Vấn đề toán học này khó ở chỗ: một số nguyên dương có thể nằm trong nhiều Bộ Ba Pythagoras khác nhau. Ví dụ như số 5, ta có dãy 3-4-5 là Bộ Ba Pythagoras, nhưng dãy 5-12-13 cũng vậy. Áp dụng điều kiện của Graham, nếu số 5 của dãy đầu tiên tô màu xanh, thì trong dãy thứ hai nó cũng phải là màu xanh, vì thế số 12 và 13 phải mang màu đỏ.

Càng tiến xa hơn với điều kiện mà Graham đề ra, các con số càng lớn và vấn đề bắt đầu nảy sinh. Nếu như số 12 phải mang màu đỏ trong dãy 5-12-13, những dãy số sau này chứa số 12 sẽ bắt buộc mang một màu nhất định.

Các nhà toán học Marijn Heule từ Đại học Texas, Victor Marek từ Đại học Kentucky, và Oliver Kullmann từ Đại học Swansea tại Anh đã cùng nhau giải quyết vấn đề này. Họ đã cài đặt một số phép thử và kĩ thuật tính toán vào trong siêu máy tính Stampede tại Đại học Texas, để cho nó có thể thu hẹp phạm vi “tô màu” xuống còn 102,300 tỷ tỷ khả năng (trăm nghìn tỷ tỷ, từng đó là có tổng cộng 25 số “0” đó các bạn).

Bộ siêu máy tính gồm 800 vi xử lý mạnh mẽ đã phải mất tới 2 ngày để “nhằn” hết đống phép thử kia, và nó chỉ có thể khả thi cho tới số 7.824. Bắt đầu từ 7.825 trở đi là không thể thỏa mãn điều kiện đặt ra của Graham.

Vậy là 3 nhà toán học (kèm một cái siêu máy tính) đã giải quyết được vấn đề toán học đã tồn tại cả thập kỉ này, và cụ Ronald Graham cũng đã giữ lời hứa của mình, thưởng “hậu hĩnh” món tiền 100 USD cho 3 anh.

“Bộ ba nguyên tử” của 3 nhà toán học này đã tạo ra một bản nén 68 gigabyte cho bất kì bạn trẻ nào có một bộ vi xử lý tốt cùng với 30.000 giờ rảnh rỗi để tải về, tái dựng và xác minh vấn đề. Nhưng nếu bạn có 30.000 giờ rảnh thật thì cũng còn một vấn đề khác nữa, con người không thể đọc được những dòng thuật toán đó.

Thực tế, bộ ba đã phải “nhờ” một chương trình máy tính khác để xác minh lại kết quả của họ, và cuối cùng thì 7.824 là con số chính xác. Ronald Graham cũng hài lòng với việc xác minh được con số này.

Nhưng nhiều người cho rằng, con người không đọc nổi kết quả nên nó không đủ thuyết phục. Dù không chứng minh được là nó sai, nhưng việc đó cũng không giải quyết vấn đề đến tận cùng. Tại sao bắt đầu từ số 7.825 trở đi thì việc “tô màu” là bất khả thi? Chúng ta không giải thích được, mà chỉ được dàn siêu máy tính kia cho biết vậy thôi.

Làm sau mà con người có thể hiểu được ý nghĩa của các con số với chúng ta cũng như với cả Vũ trụ nếu như mọi vấn đề toán học được giải quyết bằng máy như vậy. Sự thực là vấn đề này quá khó giải quyết, có lẽ cũng lại phải nhờ một bộ siêu máy tính nào đó vào cuộc thôi.

?
 

Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các bài toán hay lên diễn đàn;

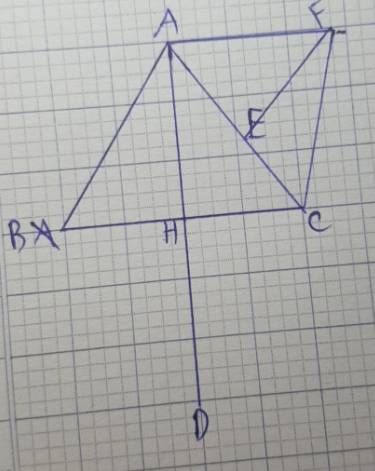
a: ΔABC cân tại A

mà AH là đường cao

nên H là trung điểm của BC

Xét tứ giác ABDC có

H là trung điểm chung của AD và BC

nên ABDC là hình bình hành

Hình bình hành ABDC có AB=AC

nên ABDC là hình thoi

b: H là trung điểm của BC

=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)

ΔAHB vuông tại H

=>\(AH^2+HB^2=AB^2\)

=>\(AH^2=5^2-3^2=16\)

=>AH=4(cm)

AD=2*AH

=>AD=2*4=8(cm)

c: 

Xét tứ giác AHCF có

E là trung điểm chung của AC và HF

nên AHCF là hình bình hành

Hình bình hành AHCF có \(\widehat{AHC}=90^0\)

nên AHCF là hình chữ nhật

=>AH\(\perp\)AF và HC\(\perp\)FC

d: ABDC là hình thoi

=>\(\widehat{BAC}=\widehat{BDC}=60^0\)

ABDC là hình thoi

=>\(\widehat{ABD}+\widehat{BAC}=180^0\)

=>\(\widehat{ABD}=120^0\)

ABDC là hình thoi

=>\(\widehat{ABD}=\widehat{ACD}=120^0\)

Bài nào v ạ