Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\Omega = \left\{ {TGT;TTG;TTT;TGG;GGT;GTG;GTT;GGG} \right\}\) nên suy ra \(n\left( \Omega \right) = 8\).
a) Ta có \(A = \left\{ {GGT;GTG;GTT;GGG} \right\}\). Suy ra \(n\left( A \right) = 4\).
Từ đó, \(P\left( A \right) = \frac{4}{8} = \frac{1}{2}\).
b) Gọi biến cố \(B\): “Có ít nhất một con trai”.
Ta có \(B = \left\{ {TGT;TTG;TTT;TGG;GGT;GTG;GTT} \right\}\). Suy ra \(n\left( B \right) = 7\).
Từ đó, \(P\left( B \right) = \frac{7}{8}\).

a) Sơ đồ cây trong đó B là ngày có mưa và A là nhà không mưa.
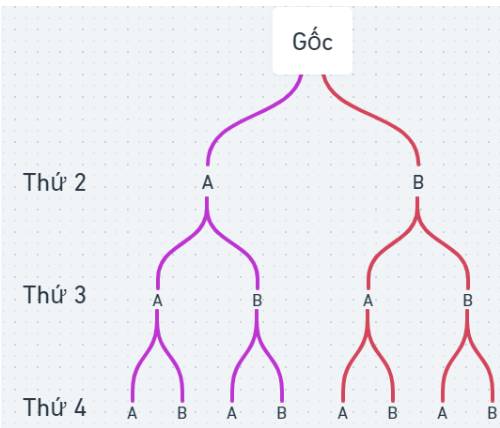
Dựa vào sơ đồ cây ta thấy \(n\left( \Omega \right) = 8\).
b) Ta có \(F = \left\{ {AAB,ABA,BAA} \right\}\). Vậy \(P\left( F \right) = \frac{3}{8}\).
\(G = \left\{ {AAB,ABA,BAA,AAA} \right\}\). Vậy \(P\left( G \right) = \frac{1}{2}\).

a) Sơ đồ cây:
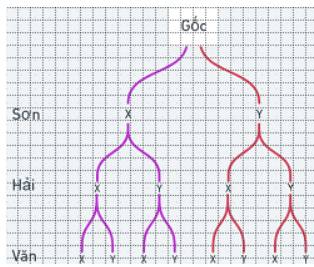
b) Dựa vào sơ đồ cây ta có \(n\left( \Omega \right) = 8\).
Gọi F là biến cố: “Hai bạn vào quán X, bạn còn lại vào quán Y”.
Ta có \(F = \left\{ {XXY;XYX;YXX} \right\}\). Suy ra \(n\left( F \right) = 3\). Vậy \(P\left( F \right) = \frac{3}{8}\).

a) Sơ đồ cây
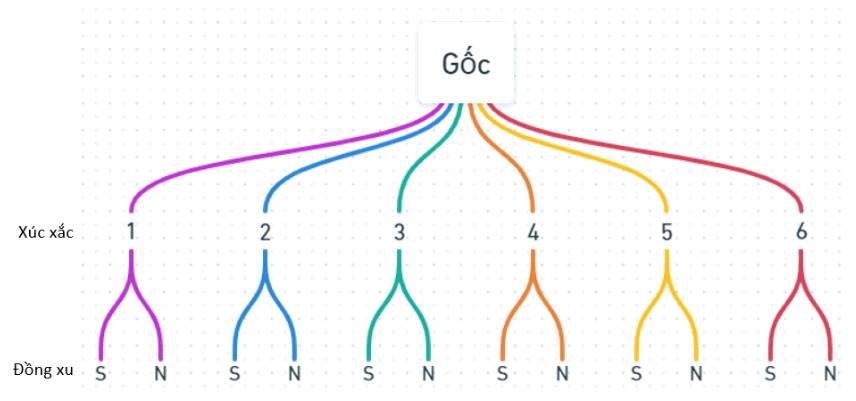
b) Từ sơ đồ cây ta có \(n\left( \Omega \right) = 12\).
Ta có \(F = \left\{ {\left( {1,N} \right);\left( {2,N} \right);\left( {3,N} \right);\left( {4,N} \right);\left( {5,N} \right);\left( {6,N} \right)} \right\}\). Suy ra \(n\left( F \right) = 6\). Vậy \(P\left( F \right) = \frac{6}{{12}} = 0,5\).
\(G = \left\{ {\left( {1,S} \right);\left( {2,S} \right);\left( {3,S} \right);\left( {4,S} \right);\left( {5,S} \right);\left( {6,S} \right);\left( {5,N} \right)} \right\}\). Suy ra \(n\left( G \right) = 7\). Vậy \(P\left( G \right) = \frac{7}{{12}}\).

Đáp án B
Dựa vào bảng số liệu ta thấy tổng các gia đình có số con lớn hơn 2 là: 5 + 2+ 1 = 8
Do đó, có 8 gia đình không đạt danh hiệu gia đình văn hóa mới

Đơn vị điều tra là số con trong mỗi gia đình và kích thước mẫu là 20 ( điều tra 20 gia đình ở tầng 2) .
Chọn B

a) Bảng phân bố tần số và tần suất:
| Số con | Tần số | Tần suất |
| 0 | 8 | 13,6% |
| 1 | 13 | 22% |
| 2 | 19 | 32,2% |
| 3 | 13 | 22% |
| 4 | 6 | 10,2% |
| Cộng | 59 | 100% |
b) Nhận xét: Hầu hết các gia đình có từ 1 đến 3 con.
Số gia đình có 2 con là nhiều nhất.
c) Số trung bình cộng:
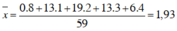
Mốt: M0 = 2 (có tần số lớn nhất bằng 19).
Sắp xếp dãy số liệu theo thứ tự không giảm:
0; 0; 0; …; 0; 1; 1; ….; 1; 2; 2; …; 2; 3; 3; …; 3; 4; 4; …; 4
Có 59 số liệu nên số trung vị là số thứ 30 trong dãy trên.
Số thứ 30 là 2 nên số trung vị Me = 2.

Tham khảo:
a) Vẽ sơ đồ cây ba tầng.
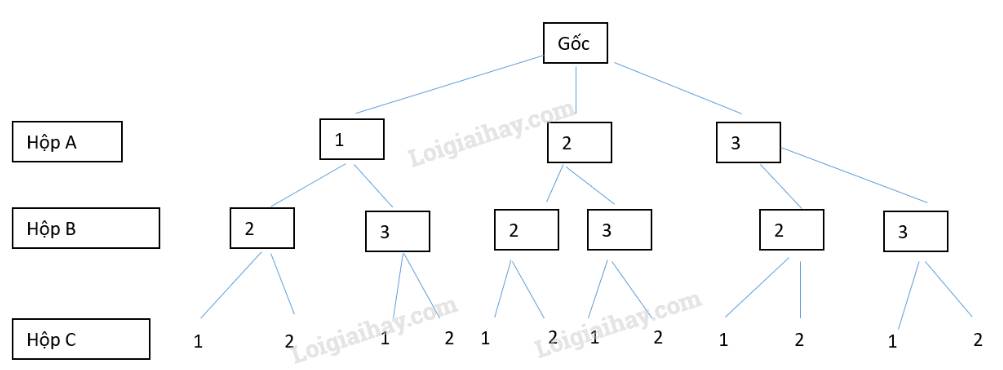
b) Chuyển qua biến cố đối: Từ sơ đồ cây xác định không gian mẫu và biến cố \(\overline M \): “Trong ba thẻ rút ra không có thẻ số 1”.
\(\begin{array}{l}\overline M = \left\{ {222;232;322;332} \right\}\\c, n(\overline M ) = 4\\P(\overline M ) = \frac{{n(\overline M )}}{{n(\Omega )}} = \frac{4}{{12}} = \frac{1}{3}\\ \Rightarrow P(M) = 1 - P(\overline M ) = 1 - \frac{1}{3} = \frac{2}{3}\end{array}\)

Đáp án A
Dựa vào bảng số liệu ta thấy, giá trị 0 có tần số lớn nhất là 10
Do đó, mốt của mẫu số liệu trên là: 0

a, Sơ đồ tư duy:
Kí hiệu con trai: T, con gái: G.
Các kết quả có thể xảy ra là: GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT.
Do đó: \(\Omega\)= {GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT}.
Vậy n(Ω) = 8.
b) Gọi biến cố A: “Gia đình đó có một con trai và hai con gái”.
Ta có: A = {GTG; TGG; GGT}. Do đó, \(n(A)\)= 3.
Vậy \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{3}{8}\)