Đáp án: C

Ta có:

(C): x 2  + y 2  + 2x + 4y = 0 ⇔ (x + 1 ) 2  + (y + 2 ) 2  = 5

⇒ I(-1;-2), R = 5

Vì d’ song song với d nên d': 2x + y + c = 0, (c ≠ -3)

Đường thẳng d’ tiếp xúc với (C) nên

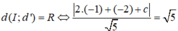
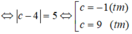
Vậy phương trình đường thẳng d’ là: 2x + y - 1 = 0 hoặc 2x + y + 9 = 0

Đáp án C

- Đường thẳng d’ song song với d nên có dạng: 3x+ y+ m= 0

- IH là khoảng cách từ I đến d’:

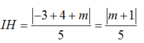
- Xét tam giác vuông IHB:

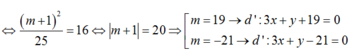
Đáp án: B

(C): x 2  + y 2  - 2x + 6y + 8 = 0

⇔ (x - 1 ) 2  + (y + 3 ) 2  = 2 có I(1;-3), R = 2

Gọi d’ là tiếp tuyến của đường tròn (C) và song song với d

Vì d'//d ⇒ d': x + y + c = 0, (c ≠ 4)

d’ là tiếp tuyến của (C) nên d(I;d') = R

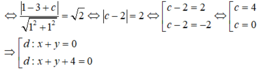
Đáp án B

Đường tròn (C) có tâm I( 1; -3) và R= 2

 có phương trình  4x- 3y+ m= 0.

Vẽ

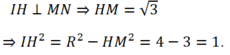
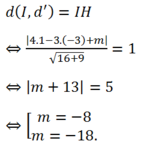
Vậy:

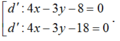
Đường tròn (C) tâm I(1;-3) bán kính \(R=4\)

Tiếp tuyến d vuông góc với 6x+8y-3=0 nên nhận \(\left(4;-3\right)\) là 1 vtpt

Tiếp tuyến d có dạng: \(4x-3y+c=0\)

\(d\left(I;d\right)=R\Leftrightarrow\dfrac{\left|4.1-3.\left(-3\right)+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=4\)

\(\Leftrightarrow\left|c+13\right|=20\Rightarrow\left[{}\begin{matrix}c=7\left(loại\right)\\c=-33\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a=4\\b=-3\\c=-33\end{matrix}\right.\)

1.

\(\left(C\right):x^2+y^2-2x-4=0\)

\(\Leftrightarrow\left(x-1\right)^2+y^2=5\)

Đường tròn \(\left(C\right)\) có tâm \(I=\left(1;0\right)\), bán kính \(R=\sqrt{5}\)

Phương trình đường thẳng \(d_1\) có dạng: \(x+y+m=0\left(m\in R\right)\)

Mà \(d_1\) tiếp xúc với \(\left(C\right)\Rightarrow d\left(I;d_1\right)=\dfrac{\left|1+m\right|}{\sqrt{2}}=\sqrt{5}\)

\(\Leftrightarrow\left|m+1\right|=\sqrt{10}\)

\(\Leftrightarrow m=-1\pm\sqrt{10}\)

\(\Rightarrow\left[{}\begin{matrix}d_1:x+y-1+\sqrt{10}=0\\d_1:x+y-1-\sqrt{10}=0\end{matrix}\right.\)

2.

Phương trình đường thẳng \(\Delta\) có dạng: \(x-y+m=0\left(m\in R\right)\)

Ta có: \(d\left(I;\Delta\right)=\sqrt{R^2-\dfrac{MN^2}{4}}=2\)

\(\Leftrightarrow\dfrac{\left|m+1\right|}{\sqrt{2}}=2\)

\(\Leftrightarrow m=-1\pm2\sqrt{2}\)

\(\Rightarrow\left[{}\begin{matrix}\Delta:x-y+1+2\sqrt{2}=0\\\Delta:x-y+1-2\sqrt{2}=0\end{matrix}\right.\)

1: Gọi I(0,y) là tâm cần tìm

Theo đề, ta có: IA=IB

=>\(\left(0-3\right)^2+\left(5-y\right)^2=\left(1-0\right)^2+\left(-7-y\right)^2\)

=>y^2-10y+25+9=y^2+14y+49+1

=>-10y+34=14y+50

=>-4y=16

=>y=-4

=>I(0;-4)

=>(x-0)^2+(y+4)^2=IA^2=90

2: Gọi (d1) là đường thẳng cần tìm

Vì (d1)//(d) nên (d1): 4x+3y+c=0

Theo đề, ta có: d(I;(d1))=3 căn 10

=>\(\dfrac{\left|0\cdot4+\left(-4\right)\cdot3+c\right|}{5}=3\sqrt{10}\)

=>|c-12|=15căn 10

=>\(\left[{}\begin{matrix}c=15\sqrt{10}+12\\c=-15\sqrt{10}+12\end{matrix}\right.\)

(d')//(d)

=>(d'): 4x-3y+c=0

(C): x^2-4x+4+y^2+6y+9-16=0

=>(x-2)^2+(y+3)^2=16

=>R=4; I(2;-3)

Theo đề, ta có: d(I;(d'))=4

=>\(\dfrac{\left|2\cdot4+\left(-3\right)\cdot\left(-3\right)+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=4\)

=>|c+17|=4*5=20

=>c=3 hoặc c=-37

(C): x^2+y^2+4x-2y-4=0

=>(x+2)^2+(y-1)^2=9

=>I(-2;1); R=3

M thuộc d nên M(a;1-a)

M nằm ngoài (C) nên IM>R

=>IM^2>9

=>2a^2+4a-5>0

MA^2=MB^2=IM^2-IA^2=(a+2)^2+(-a)^2-9=2a^2+4a-5

=>x^2+y^2-2ax+2(a-1)y-6a+6=0(1)

A,B thuộc (C)

=>Tọa độ A,B thỏa mãn phương trình:

 x^2+y^2+4x-2y-4=0(2)

(1)-(2)=(a+2)x-ay+3a-5=0(3)

Tọa độ A,B thỏa mãn (3) nên (3) chính là phương trình đường thẳng AB

(E) tiếp xúc AB nên (E): R1=d(E,AB)

Chu vi của (E) lớn nhất khi R1 lớn nhất

=>d(E;AB) lớn nhất

Gọi H là hình chiếu vuông góc của E lên AB

=>d(E,Δ)=EH<=EK=căn 10/2

Dấu = xảy ra khi H trùng K

=>AB vuông góc EK

vecto EK=(-1/2;3/2), AB có VTCP là (a;a+2)

AB vuông góc EK

=>-1/2a+3/2(a+2)=0

=>a=-3

=>M(-3;4)