

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A
+ Điều kiện để hệ ba vân sáng này trùng nhau: k1λ1 = k2λ2 = k3λ3 ↔ 4k1 = 5k2 = 6k3
Bội chung nhỏ nhất của ba số hạng trên là 60, ứng với vị trí trùng nhau gần vân trung tâm nhất:
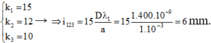
+ Xét tỉ số O M i 123 = 7 6 ≈ 1 , 16 → trên đoạn OM chỉ có 2 vân trùng màu với nguồn

\(i_1 = \frac{\lambda_1 D}{a}\\ i_2 = \frac{\lambda_2 D}{a}\)=> \( \frac{i_1}{i_2}= \frac{\lambda _1}{\lambda_2}= \frac{540}{600}=0,9.\)
=> \(i_2 = \frac{i_1}{0,9}=0,4 mm.\)

Đáp án B
+ Khoảng vân giao thoa của các ánh sáng đơn sắc

+ Ta xét các tỉ số:
x M i 1 = 3 , 3 x M i 1 = 13 , 3 → trên đoạn MN có các vị trí cho vân sáng từ bậc 4 đến bậc 13 của bức xạ λ1
x M i 2 = 2 , 56 x M i 2 = 10 , 25 → trên đoạn MN có các vị trí cho vân sáng từ bậc 3 đến bậc 10 của bức xạ λ2
+ Điều kiện trùng nhau của hai hệ vân
λ 1 λ 2 = k 2 k 1 = 10 13 → trên đoạn MN có một vị trí trùng nhau của hệ hai vân sáng, do đó số vân sáng quan sát được là
n
=
10
+
8
-
1
=
17
(ta trừ một là do hai vân sáng trùng nhau ta tính là một vân sáng)