Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Coi sự giao thoa trùng vân giống như giao thoa ánh sáng đơn sắc, ta đi tìm khoảng vân trùng nhau.
Cách giải:
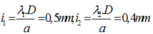
Vị trí vân sáng và vân tối thỏa mãn điều kiện :
![]()
Vì vân sáng trùng với vị trí vân tối nên ta có:
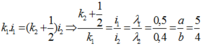
Coi đây là hiện tượng giao thoa với khoảng vân trùng nhau là:
![]()
Số vân trùng nhau trong khoảng MN thỏa mãn điều kiện :
![]()
![]()
![]()
Vậy có 15 giá trị k thỏa mãn

Đáp án C
+ Điều kiện để có sự trùng nhau của hai hệ vân sáng
.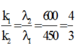
![]()
Xét tỉ số
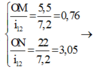 có 3 vân trùng.
có 3 vân trùng.

Chọn C
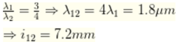
Vậy trên đoạn MN có 3 vị trí vân sáng trùng nhau (7.2, 14.4, 21.6)

Đáp án C
+ Khoảng vân giao thoa của hai bức xạ
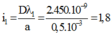 ;
;
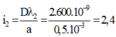
+ Các vị trí hệ hai vân sangs trùng nhau

mm cứ sau mỗi khoảng
![]()
lại có một vị trí trùng nhau của hệ hai vân sang.
Xét tỉ số 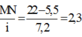
=> có hai vân sáng trùng nhau.

Phương pháp: Sử dụng lí thuyết bài toán giao thoa nhiều ánh sáng
Cách giải:
Số vân sáng của bức xạ đơn sắc 1 thu được trên màn
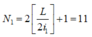
Số vân sáng của bức xạ đơn sắc 2 thu được trên màn

Xét sự trùng nhau của hai bức xạ
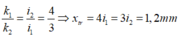
Số vân sáng trùng nhau của hai bức xạ là
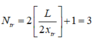
Số vân sáng quan sát được trên màn là N = N1 + N2 – Ntr = 11 + 7 – 3 = 15 vân sáng
Chọn A

Đáp án A
Số vân sáng của bức xạ đơn sắc 1 thu được trên màn
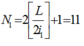
Số vân sáng của bức xạ đơn sắc 2 thu được trên màn
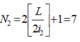
Xét sự trùng nhau của hai bức xạ
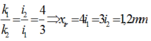
Số vân sáng trùng nhau của hai bức xạ là
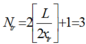
Số vân sáng quan sát được trên màn là N = N1 + N2 – Ntr = 11 + 7 – 3 = 15 vân sáng

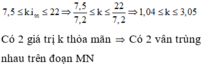

Đáp án: 23 vị trí; 0,6mm.
Cách 1:
- Vân sáng của i1 trùng với vân tối của i2 →2i1 = 0,6mm; i2 = 0,4; i0 = 1,2mm;
- Ta có kM = -4,6; kN = 18,3. Số giá trị k bán nguyên là : 17,5 + 4,5 + 1 = 23 giá trị.
Cách 2:
+ Vân sáng của λ1 trùng với vân sáng của λ2: \(\frac{k_1}{k_2}=\frac{i_1}{i_2}=\frac{4}{3}\)
\(\Rightarrow\) Vân sáng có tọa độ 4ki1 của λ1 trùng với vân sáng có tọa độ 3ki2của λ2
\(\Rightarrow\) Vân sáng có tọa độ 2ki1 của λ1 trùng với vân sáng có tọa độ 1,5 ki2của λ2 (k lẻ)
\(\Rightarrow\) xtrùng = \((k+\frac{1}{2})4i_1(mm) \Rightarrow 5,5\leq(k+\frac{1}{2})4i_1\leq 2,2.10\)
\(\Leftrightarrow{-5,08}\leq{k}\leq{17,8}\)
\(\Rightarrow\) có 23 vị trí thỏa mãn.
Khoảng cách gần nhất từ điểm thỏa mãn đến vân trung tâm tương ứng với k = 0
xmin = 0,5.4i1 = 0,6 (mm)